题目内容
抛物线y=-x2+2x+3与x轴交于A、B两点(A在B的左侧),与y轴交于点D,顶点为C
(1)求A、B、C、D各点坐标;
(2)求四边形ABCD的面积;
(3)抛物线上是否存在点P,使△PAB的面积是△ABC的面积的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)求A、B、C、D各点坐标;
(2)求四边形ABCD的面积;
(3)抛物线上是否存在点P,使△PAB的面积是△ABC的面积的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)∵y=-x2+2x+3=-(x+1)(x-3)=-(x-1)2+4,
∴A(-1,0)、B(3,0)、C(1,4)、D(0,3).
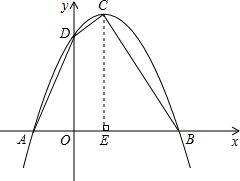 (2)过C作CE⊥x轴,垂足为E;
(2)过C作CE⊥x轴,垂足为E;
由(1)知:OA=1、OD=3、CE=4、OE=1、BE=2;
S四边形ABCD=S△AOD+S△BCE+S梯形ODCE
=
×1×3+
×2×4+
×(3+4)×1=9.
(3)由于CE=4,即点C到x轴的距离为4;
若S△PAB=2S△ABC,则点P到x轴的距离为8,
设P(x,-8),依题意,有:
-x2+2x+3=-8,
化简得:x2-2x-11=0
解得:x=1±2
;
即:P(1±2
,-8).
∴A(-1,0)、B(3,0)、C(1,4)、D(0,3).
 (2)过C作CE⊥x轴,垂足为E;
(2)过C作CE⊥x轴,垂足为E;由(1)知:OA=1、OD=3、CE=4、OE=1、BE=2;
S四边形ABCD=S△AOD+S△BCE+S梯形ODCE
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由于CE=4,即点C到x轴的距离为4;
若S△PAB=2S△ABC,则点P到x轴的距离为8,
设P(x,-8),依题意,有:
-x2+2x+3=-8,
化简得:x2-2x-11=0
解得:x=1±2
| 3 |
即:P(1±2
| 3 |

练习册系列答案
相关题目


 y=x2-mx+n,若方程x2-mx+n=0两根倒数和为-2.
y=x2-mx+n,若方程x2-mx+n=0两根倒数和为-2.