Question

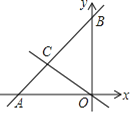
【题目】如图，在四边形中，，对角线与相交于点，分别是边、的中点.

（1）求证：；

（2）当时，求的长.

Answer 1

【答案】（1）证明见解析；（2）2.5

【解析】

（1）连接BM、DM，根据直角三角形斜边上 的中线的性质求出BM=DM，根据等腰三角形性质求出即可；

（2）根据等腰三角形性质和三角形外角性质求出∠BMN=30°，求出∠NBM=30°，求BM，根据直角三角形的性质求出即可．

证明：（1）连接BM、DM．

∵∠ABC=∠ADC=90°，点M、点N分别是边AC、BD的中点，

∴BM=AC，CM=AC，

∴BM＝DM＝AC，

∵N是BD的中点，

∴MN是BD的垂直平分线，

∴MN⊥BD

（2）解：∵∠BCA=15°，BM＝CM＝AC，

∴∠BCA=∠CBM=15°，

∴∠BMA=30°，

∵OB=OM，

∴∠OBM=∠BMA=30°，

∵AC=10，BM＝AC，

∴BM=5，

在Rt△BMN中，∠BNM=90°，∠NBM=30°，

∴MN＝BM＝2.5，

答：MN的长是2.5．