题目内容
【题目】如图所示，在
中，
是边
中点，连接
，将
沿线段翻折后得
，其中
，则到
边的距离为（ ）
A.
B.
C.
D.
【答案】D
【解析】
首先连接AA′，延长BD与AA′交于点E，作DF⊥AB，由翻折的性质得出△ABA′为等腰三角形，△A′CD是等边三角形，然后利用等腰三角形三线合一的性质得出BE⊥AA′，AE=A′E，进而利用勾股定理得出DE、BD，再次利用勾股定理构建方程，即可得出AF，进而得出DF.
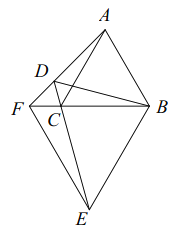
连接AA′，延长BD与AA′交于点E，作DF⊥AB于F，如图所示：
由已知，得AB=A′B=
，AD=A′D=4
∴△ABA′为等腰三角形，
∴BE⊥AA′，AE=A′E
∵A′C=4
∴△A′CD是等边三角形
∴∠ADA′=120°，∠EDA′=60°，∠AA′C=90°
∴DE=2，AE=A′E=
∴
∴BD=BE-DE=5-2=3
设AF=
，在△ABD中，
∴
即
解得
∴
故答案为D.
练习册系列答案
相关题目
