ЬтФПФкШн
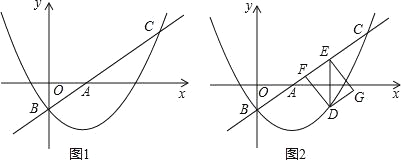
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпlЃКy=![]() x+mгыxжсЁЂyжсЗжБ№НЛгкЕуAКЭЕуBЃЈ0ЃЌЉ1ЃЉЃЌХзЮяЯпy=
x+mгыxжсЁЂyжсЗжБ№НЛгкЕуAКЭЕуBЃЈ0ЃЌЉ1ЃЉЃЌХзЮяЯпy=![]() x2+bx+cОЙ§ЕуBЃЌгыжБЯпlЕФСэвЛИіНЛЕуЮЊCЃЈ4ЃЌnЃЉЃЎ
x2+bx+cОЙ§ЕуBЃЌгыжБЯпlЕФСэвЛИіНЛЕуЮЊCЃЈ4ЃЌnЃЉЃЎ
ЃЈ1ЃЉЧѓnЕФжЕКЭХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуDдкХзЮяЯпЩЯЃЌDEЁЮyжсНЛжБЯпlгкЕуEЃЌЕуFдкжБЯпlЩЯЃЌЧвЫФБпаЮDFEGЮЊОиаЮЃЈШчЭМ2ЃЉЃЌЩшЕуDЕФКсзјБъЮЊtЃЈ0ЃМtЃМ4ЃЉЃЌОиаЮDFEGЕФжмГЄЮЊpЃЌЧѓpгыtЕФКЏЪ§ЙиЯЕЪНвдМАpЕФзюДѓжЕЃЛ
ЃЈ3ЃЉНЋЁїAOBШЦЦНУцФкФГЕуMа§зЊ90ЁуЛђ180ЁуЃЌЕУЕНЁїA1O1B1ЃЌЕуAЁЂOЁЂBЕФЖдгІЕуЗжБ№ЪЧЕуA1ЁЂO1ЁЂB1ЃЎШєЁїA1O1B1ЕФСНИіЖЅЕуЧЁКУТфдкХзЮяЯпЩЯЃЌФЧУДЮвУЧОЭГЦетбљЕФЕуЮЊЁАТфЕуЁБЃЌЧыжБНгаДГіЁАТфЕуЁБЕФИіЪ§КЭа§зЊ180ЁуЪБЕуA1ЕФКсзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉn=2ЃЛy=![]() x2Љ
x2Љ![]() xЉ1ЃЛЃЈ2ЃЉp=
xЉ1ЃЛЃЈ2ЃЉp=![]() ЃЛЕБt=2ЪБЃЌpгазюДѓжЕ
ЃЛЕБt=2ЪБЃЌpгазюДѓжЕ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉАбЕуBЕФзјБъДњШыжБЯпНтЮіЪНЧѓГіmЕФжЕЃЌдйАбЕуCЕФзјБъДњШыжБЯпЧѓНтМДПЩЕУЕНnЕФжЕЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪННтД№ЃЛ
ЃЈ2ЃЉСюy=0ЧѓГіЕуAЕФзјБъЃЌДгЖјЕУЕНOAЁЂOBЕФГЄЖШЃЌРћгУЙДЙЩЖЈРэСаЪНЧѓГіABЕФГЄЃЌШЛКѓИљОнСНжБЯпЦНааЃЌФкДэНЧЯрЕШПЩЕУЁЯABO=ЁЯDEFЃЌдйНтжБНЧШ§НЧаЮгУDEБэЪОГіEFЁЂDFЃЌИљОнОиаЮЕФжмГЄЙЋЪНБэЪОГіpЃЌРћгУжБЯпКЭХзЮяЯпЕФНтЮіЪНБэЪОDEЕФГЄЃЌећРэМДПЩЕУЕНPгыtЕФЙиЯЕЪНЃЌдйРћгУЖўДЮКЏЪ§ЕФзюжЕЮЪЬтНтД№ЃЛ
ЃЈ3ЃЉИљОнФцЪБеыа§зЊНЧЮЊ90ЁуПЩЕУA1O1ЁЮyжсЪБЃЌB1O1ЁЮxжсЃЌа§зЊНЧЪЧ180ЁуХаЖЯГіA1O1ЁЮxжсЪБЃЌB1A1ЁЮABЃЌИљОнЭМ3ЁЂЭМ4СНжжЧщаЮМДПЩНтОіЃЎ
НтЃК
ЃЈ1ЃЉЁпжБЯпlЃКy=![]() x+mОЙ§ЕуBЃЈ0ЃЌЉ1ЃЉЃЌ
x+mОЙ§ЕуBЃЈ0ЃЌЉ1ЃЉЃЌ
Ёрm=Љ1ЃЌ
ЁржБЯпlЕФНтЮіЪНЮЊy=![]() xЉ1ЃЌ
xЉ1ЃЌ
ЁпжБЯпlЃКy=![]() xЉ1ОЙ§ЕуCЃЈ4ЃЌnЃЉЃЌ
xЉ1ОЙ§ЕуCЃЈ4ЃЌnЃЉЃЌ
Ёрn=![]() ЁС4Љ1=2ЃЌ
ЁС4Љ1=2ЃЌ
ЁпХзЮяЯпy=![]() x2+bx+cОЙ§ЕуCЃЈ4ЃЌ2ЃЉКЭЕуBЃЈ0ЃЌЉ1ЃЉЃЌ
x2+bx+cОЙ§ЕуCЃЈ4ЃЌ2ЃЉКЭЕуBЃЈ0ЃЌЉ1ЃЉЃЌ
Ёр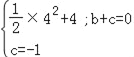 ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=![]() x2Љ
x2Љ![]() xЉ1ЃЛ
xЉ1ЃЛ
ЃЈ2ЃЉСюy=0ЃЌдђ![]() xЉ1=0ЃЌ
xЉ1=0ЃЌ
НтЕУx=![]() ЃЌ
ЃЌ
ЁрЕуAЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁрOA=![]() ЃЌ
ЃЌ
дкRtЁїOABжаЃЌOB=1ЃЌ
ЁрAB=![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ЁпDEЁЮyжсЃЌ
ЁрЁЯABO=ЁЯDEFЃЌ
дкОиаЮDFEGжаЃЌEF=DEcosЁЯDEF=DE![]() =
=![]() DEЃЌ
DEЃЌ
DF=DEsinЁЯDEF=DE![]() =
=![]() DEЃЌ
DEЃЌ
Ёрp=2ЃЈDF+EFЃЉ=2ЃЈ![]() +
+![]() ЃЉDE=
ЃЉDE=![]() DEЃЌ
DEЃЌ
ЁпЕуDЕФКсзјБъЮЊtЃЈ0ЃМtЃМ4ЃЉЃЌ
ЁрDЃЈtЃЌ![]() t2Љ
t2Љ![]() tЉ1ЃЉЃЌEЃЈtЃЌ
tЉ1ЃЉЃЌEЃЈtЃЌ![]() tЉ1ЃЉЃЌ
tЉ1ЃЉЃЌ
ЁрDE=ЃЈ![]() tЉ1ЃЉЉЃЈ
tЉ1ЃЉЉЃЈ![]() t2Љ
t2Љ![]() tЉ1ЃЉ=Љ
tЉ1ЃЉ=Љ![]() t2+2tЃЌ
t2+2tЃЌ
Ёрp=![]() ЁСЃЈЉ
ЁСЃЈЉ![]() t2+2tЃЉ=Љ
t2+2tЃЉ=Љ![]() t2+
t2+![]() tЃЌ
tЃЌ
Ёпp=Љ![]() ЃЈtЉ2ЃЉ2+
ЃЈtЉ2ЃЉ2+![]() ЃЌЧвЉ
ЃЌЧвЉ![]() ЃМ0ЃЌ
ЃМ0ЃЌ
ЁрЕБt=2ЪБЃЌpгазюДѓжЕ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЁАТфЕу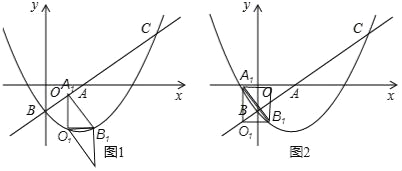
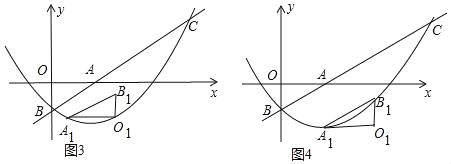
ШчЭМ3жаЃЌЩшA1ЕФКсзјБъЮЊmЃЌдђO1ЕФКсзјБъЮЊm+![]() ЃЌ
ЃЌ
Ёр![]() m2Љ
m2Љ![]() mЉ1=
mЉ1=![]() ЃЈm+
ЃЈm+![]() ЃЉ2Љ
ЃЉ2Љ![]() ЃЈm+
ЃЈm+![]() ЃЉЉ1ЃЌ
ЃЉЉ1ЃЌ
НтЕУm=![]() ЃЌ
ЃЌ
ШчЭМ4жаЃЌЩшA1ЕФКсзјБъЮЊmЃЌдђB1ЕФКсзјБъЮЊm+![]() ЃЌB1ЕФзнзјБъБШР§A1ЕФзнзјБъДѓ1ЃЌ
ЃЌB1ЕФзнзјБъБШР§A1ЕФзнзјБъДѓ1ЃЌ
Ёр![]() m2Љ
m2Љ![]() mЉ1+1=
mЉ1+1=![]() ЃЈm+
ЃЈm+![]() ЃЉ2Љ
ЃЉ2Љ![]() ЃЈm+
ЃЈm+![]() ЃЉЉ1ЃЌ
ЃЉЉ1ЃЌ
НтЕУm=![]() ЃЌ
ЃЌ
Ёра§зЊ180ЁуЪБЕуA1ЕФКсзјБъЮЊ![]() Лђ
Лђ![]()

 ВНВНИпДяБъОэЯЕСаД№АИ
ВНВНИпДяБъОэЯЕСаД№АИЁОЬтФПЁПФГЩЬЕъвЛжмФкМзЁЂввСНжжМЦЫуЦїУПЬьЕФЯњЪлСПШчЯТЃЈЕЅЮЛЃКИіЃЉЃК
РрБ№/аЧЦк | вЛ | Жў | Ш§ | ЫФ | Юх | Сљ | Цп | ЦНОљЪ§ |
Мз |
|
|
|
|
|
|
| |
вв |
|
|
|
|
|
|
|
|
ЃЈ1ЃЉНЋБэИёЬюаДЭъећЃЎ
ЃЈ2ЃЉЧѓМзжжМЦЫуЦїБОжмЯњЪлСПЕФЗНВюЃЎ
ЃЈ3ЃЉвбжЊввжжМЦЫуЦїБОжмЯњЪлСПЕФЗНВюЮЊ![]() ЃЌБОжмФФжжМЦЫуЦїЕФЯњЪлСПБШНЯЮШЖЈЃПЫЕУїРэгЩЃЎ
ЃЌБОжмФФжжМЦЫуЦїЕФЯњЪлСПБШНЯЮШЖЈЃПЫЕУїРэгЩЃЎ