Question

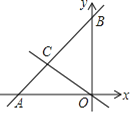
【题目】如图，一次函数的图像与轴轴分别交于点、点，函数，与的图像交于第二象限的点，且点横坐标为.

（1）求的值；

（2）当时，直接写出的取值范围；

（3）在直线上有一动点，过点作轴的平行线交直线于点，当时，求点的坐标.

Answer 1

【答案】（1）（2）（3）点坐标为或

【解析】

（1）将点横坐标代入求得点C的纵坐标为4，再把（-3，4）代入求出b即可；

（2）求出点A坐标，结合点C坐标即可判断出当时， 的取值范围；

（3）设P（a,-），可求出Q（，），即可得PQ=，再求出OC=5，根据求出a的值即可得出结论.

（1）把代入，

得.

∴C（-3，4）

把点代入，

得.

（2）∵b=7

∴y=x+7，

当y=0时，x=-7,x=-3时，y=4，

∴当时，.

（3）点为直线上一动点，

设点坐标为.

轴，

把代入，得.

点坐标为，

又点坐标为，

解之，得或.

点坐标为或.