题目内容
【题目】已知四边形ABCD是正方形,点E是边BC上的任意一点,AE⊥EF,且直线EF交正方形外角的平分线CF于点F.
(1)如图1,求证:AE=EF;
(2)如图2,当AB=2,点E是边BC的中点时,请直接写出FC的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)截取BE=BM,连接EM,求出AM=EC,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(2)取AB中点M,连接EM,求出BM=BE,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可.
(1)证明:如图1,在AB上截取BM=BE,连接ME,
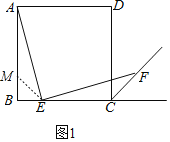
∵∠B=90°,
∴∠BME=∠BEM=45°,
∴∠AME=135°
∵CF是正方形的∠C外角的平分线,
∴∠ECF=90°+45°=135°
∴∠AME=∠ECF,
∵AB=BC,BM=BE,
∴AM=EC,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AEB+∠CEF=90°,
∵∠BAE+∠AEB=90°,
∴∠BAE=∠CEF,
在△AME和△ECF中
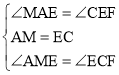 ,
,
∴△AME≌△ECF(ASA),
∴AE=EF;
(2)解:取AB中点M,连接EM,
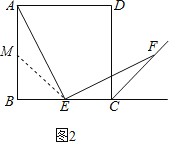
∵AB=BC,E为BC中点,M为AB中点,
∴AM=CE=BE,
∴∠BME=∠BME=45°,
∴∠AME=135°=∠ECF,
∵∠B=90°,
∴∠BAE+∠AEB=90°,
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,
∴∠BAE=∠FEC,
在△AME和△ECF中
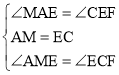 ,
,
∴△AME≌△ECF(ASA),
∴EM=CF,
∵AB=2,点E是边BC的中点,
∴BM=BE=1,
∴CF=ME=![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目