题目内容
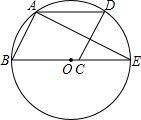
如图，CD是⊙O的直径，弦AB⊥CD于点G，直线EF与⊙O相切于点D，则下列结论中不一定正确的是（ ）
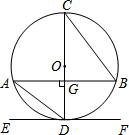
| A．AG="BG" | B．AB∥EF | C．AD∥BC | D．∠ABC=∠ADC |
C
本题考查了切线的性质定理、圆周角定理以及垂径定理，理解定理是关键．根据切线的性质，垂径定理即可作出判断．
解：A、∵CD是⊙O的直径，弦AB⊥CD于点G，∴AG=BG，故正确；
B、∵直线EF与⊙O相切于点D，∴CD⊥EF，又∵AB⊥CD，∴AB∥EF，故正确；
C、只有当弧AC=弧AD时，AD∥BC，当两个互不相等时，则不平行，故选项错误；
D、根据同弧所对的圆周角相等，可以得到∠ABC=∠ADC．故选项正确．
故选C．
解：A、∵CD是⊙O的直径，弦AB⊥CD于点G，∴AG=BG，故正确；
B、∵直线EF与⊙O相切于点D，∴CD⊥EF，又∵AB⊥CD，∴AB∥EF，故正确；
C、只有当弧AC=弧AD时，AD∥BC，当两个互不相等时，则不平行，故选项错误；
D、根据同弧所对的圆周角相等，可以得到∠ABC=∠ADC．故选项正确．
故选C．
练习册系列答案
寒假学与练系列答案
相关题目
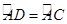，弦AB与弦AC交于点A，弦CD与AB交于点F，连 接BC．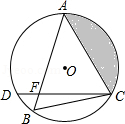
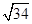，BC－AC=2，求CE的长．
