题目内容
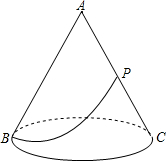
如图，□ABCD的顶点A、B、D在⊙O上，顶点C在⊙O的直径BE上，∠ADC=54°，连接AE，则∠AEB的度数为（ ）
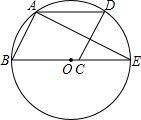
A．36° B．46° C．27° D．63°
A．36° B．46° C．27° D．63°
A
本题考查了圆周角定理及平行四边形的性质，解答本题的关键是根据平行四边形的性质得出∠B=∠ADC．根据BE是直径可得∠BAE=90°，然后在□ABCD中∠ADC=54°，可得∠B=54°，继而可求得∠AEB的度数．
解：∵四边形ABCD是平行四边形，∠ADC=54°，
∴∠B=∠ADC=54°，
∵BE为⊙O的直径，
∴∠BAE=90°，
∴∠AEB=90°﹣∠B=90°﹣54°=36°．
故选A．
解：∵四边形ABCD是平行四边形，∠ADC=54°，
∴∠B=∠ADC=54°，
∵BE为⊙O的直径，
∴∠BAE=90°，
∴∠AEB=90°﹣∠B=90°﹣54°=36°．
故选A．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
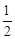∠ACB；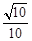
，CB=12，求⊙O 的半径及
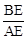的值．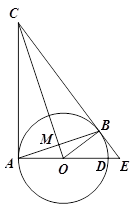
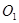的半径为1cm，⊙
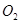的半径为3cm，两圆的圆心距
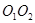为4cm，则两圆的位置关系是（ ）
π
π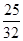
π
π