题目内容
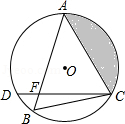
)如图所示,在⊙O中,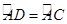 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.
(1)求证:AC2=AB•AF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
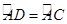 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连 接BC.(1)求证:AC2=AB•AF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.

(1)证明见解析;(2)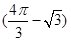 cm2.
cm2.
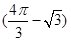 cm2.
cm2.试题分析:(1)由
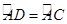 ,利用等弧所对的圆周角相等得到一对角相等,再由一对公共角相等,利用两对对应角相等的两三角形相似可得出△ACF与△ABC相似,根据相似得比例可得证;
,利用等弧所对的圆周角相等得到一对角相等,再由一对公共角相等,利用两对对应角相等的两三角形相似可得出△ACF与△ABC相似,根据相似得比例可得证;(2)连接OA,OC,利用同弧所对的圆心角等于圆周角的2倍,由∠B为60°,求出∠AOC为120°,过O作OE垂直于AC,垂足为点E,由OA=OC,利用三线合一得到OE为角平分线,可得出∠AOE为60°,在Rt△AOE中,由OA及cos60°的值,利用锐角三角函数定义求出OE的长,在Rt△AOE中,利用勾股定理求出AE的长,进而求出AC的长,由扇形AOC的面积-△AOC的面积表示出阴影部分的面积,利用扇形的面积公式及三角形的面积公式即可求出阴影部分的面积.
(1)证明:∵
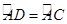 ,
,∴∠ACD=∠ABC,又∠BAC=∠CAF,
∴△ACF∽△ABC,
∴
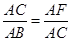 ,即AC2=AB•AF;
,即AC2=AB•AF; (2)解:连接OA,OC,过O作OE⊥AC,垂足为点E,

∵∠ABC=60°,
∴∠AOC=120°,
又OA=OC,
∴∠AOE=∠COE=
 ×120°=60°,
×120°=60°,在Rt△AOE中,OA=2cm,
∴OE=OAcos60°=1cm,
∴AE=
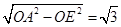 cm,
cm,∴AC=2AE=2
 cm,
cm,则S阴影=S扇形OAC﹣S△AOC=
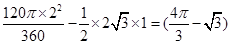 cm2.
cm2.
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
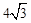 ,求⊙O的面积.
,求⊙O的面积.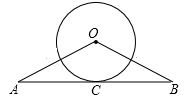
 时,
时,
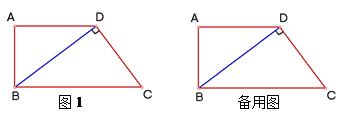
 BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.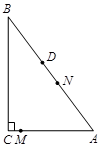
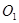 的半径为1cm,⊙
的半径为1cm,⊙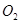 的半径为3cm,两圆的圆心距
的半径为3cm,两圆的圆心距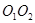 为4cm,则两圆的位置关系是( )
为4cm,则两圆的位置关系是( )