题目内容
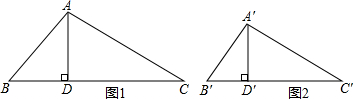
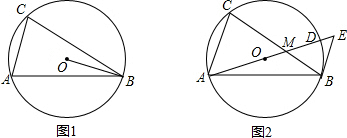
已知,⊙O为△ABC的外接圆,AB=BC.
(1)如图1,若AC=2,BC=
,求cos∠CBO的值;
(2)如图2,过B作⊙O的切线交直径AD的延长线于E,BC交AD于M,若OM:OA=2:5,求tan∠E的值.
(1)如图1,若AC=2,BC=
| 10 |
(2)如图2,过B作⊙O的切线交直径AD的延长线于E,BC交AD于M,若OM:OA=2:5,求tan∠E的值.

考点:切线的性质,勾股定理,垂径定理,锐角三角函数的定义
专题:
分析:(1)延长BO交AC于H点,由AB=CB得弧BA=弧BC,根据垂径定理的推论得BH垂直AC,且CH=AH,则CH=1,再利用勾股定理计算出BH,然后根据余弦的定义求解;
(2)和(1)一样得到BO垂直AC,OM=2a,OA=5a,则MD=3a,根据切线的性质得OB⊥BE,则AC∥BE,所以∠E=∠HAO;根据等腰三角形性质得∠MBO=∠OBA,而∠OBA=∠OAB,则∠MBO=∠MAB,于是可判断△MOB∽△MBA,利用相似比可计算出BM=
a,再根据相交弦定理可计算出MC=
a,所以BC=
a,即BA=
a,在RtABH和RtAOH中利用勾股定理可计算出OH与AH,然后根据正切的定义求解.
(2)和(1)一样得到BO垂直AC,OM=2a,OA=5a,则MD=3a,根据切线的性质得OB⊥BE,则AC∥BE,所以∠E=∠HAO;根据等腰三角形性质得∠MBO=∠OBA,而∠OBA=∠OAB,则∠MBO=∠MAB,于是可判断△MOB∽△MBA,利用相似比可计算出BM=
| 14 |
3
| ||
| 2 |
5
| ||
| 2 |
5
| ||
| 2 |
解答: 解:(1)延长BO交AC于H点,如图1,
解:(1)延长BO交AC于H点,如图1,
∵AB=CB,
∴弧BA=弧BC,
∴BH垂直AC,且CH=AH,
∴CH=
AC=1,
在Rt△BCH中,BC=
,
∴BH=
=3,
∴cos∠CBH=
=
=
,
即cos∠CBO的值为
;
(2)延长BO交AC于H点,如图2,
则BH垂直AC,且CH=AH,设OM=2a,OA=5a,则MD=3a,
∵BE为⊙O的切线,
∴OB⊥BE,
∴AC∥BE,
∴∠E=∠HAO,
∵BH平分∠ABC,
∴∠MBO=∠OBA,
而∠OBA=∠OAB,
∴∠MBO=∠MAB,
∵∠OMB=∠BMA,
∴△MOB∽△MBA,
∴OM:BM=BM:MA,即2a:BM=BM:7a,
∴BM=
a,
∵MA•MD=MB•MC,即7a•3a=
a•MC,
∴MC=
a,
∴BC=MC+MB=
a,
∴BA=
a,
在RtABH中,AB2=BH2+AH2,即(
a)2=(OH+5a)2+AH2①,
在RtAOH中,AO2=OH2+AH2,即(5a)2=OH2+AH2②,
由①②可解得OH=
a,AH=
a,
∴tan∠HAO=
=
,
∴tan∠E=
.
 解:(1)延长BO交AC于H点,如图1,
解:(1)延长BO交AC于H点,如图1,∵AB=CB,
∴弧BA=弧BC,
∴BH垂直AC,且CH=AH,
∴CH=
| 1 |
| 2 |
在Rt△BCH中,BC=
| 10 |
∴BH=
| BC2-CH2 |
∴cos∠CBH=
| BH |
| BC |
| 3 | ||
|
3
| ||
| 10 |
即cos∠CBO的值为
3
| ||
| 10 |
(2)延长BO交AC于H点,如图2,
则BH垂直AC,且CH=AH,设OM=2a,OA=5a,则MD=3a,
∵BE为⊙O的切线,
∴OB⊥BE,
∴AC∥BE,
∴∠E=∠HAO,
∵BH平分∠ABC,
∴∠MBO=∠OBA,
而∠OBA=∠OAB,
∴∠MBO=∠MAB,
∵∠OMB=∠BMA,
∴△MOB∽△MBA,
∴OM:BM=BM:MA,即2a:BM=BM:7a,
∴BM=
| 14 |
∵MA•MD=MB•MC,即7a•3a=
| 14 |
∴MC=
3
| ||
| 2 |
∴BC=MC+MB=
5
| ||
| 2 |
∴BA=
5
| ||
| 2 |
在RtABH中,AB2=BH2+AH2,即(
5
| ||
| 2 |
在RtAOH中,AO2=OH2+AH2,即(5a)2=OH2+AH2②,
由①②可解得OH=
| 15 |
| 4 |
5
| ||
| 4 |
∴tan∠HAO=
| OH |
| AH |
3
| ||
| 7 |
∴tan∠E=
3
| ||
| 7 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理、垂径定理、锐角三角函数的定义和三角形相似的判定与性质.

练习册系列答案
相关题目
下列方程中,没有实数根的方程是( )
| A、x3+1=0 | ||
| B、x4+6x2+8=0 | ||
C、
| ||
D、
|
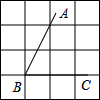 如图,在4×4的正方形网格中,∠ABC按如图所示的位置摆放,则tan∠ABC的值是( )
如图,在4×4的正方形网格中,∠ABC按如图所示的位置摆放,则tan∠ABC的值是( )A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
两个相似三角形的一组对应边分别为6cm和8cm,如果较小三角形的周长为27cm,那么较大三角形的周长为( )
| A、30cm | B、36cm |
| C、45cm | D、54cm |