题目内容
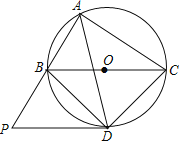
【题目】如图,在平面直角坐标系中,AB=3![]() ,连结AB并延长至C,连结OC,若满足OC2=BCAC,tanα=2,则点C的坐标为( )
,连结AB并延长至C,连结OC,若满足OC2=BCAC,tanα=2,则点C的坐标为( )
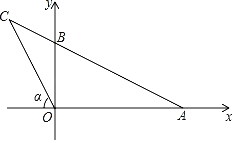
A.(﹣2,4)B.(﹣3,6)C.(﹣![]() ,
,![]() )D.(﹣
)D.(﹣![]() ,
,![]() )
)
【答案】A
【解析】
根据相似三角形的判定得到△OBC∽△OAC,则∠A=∠COB,进而得出∠ABO=α,利用tanα=2,得出OA=2OB,利用勾股定理解得OB,从而可知OA的长,进而可知tan∠A的值,由tanα=2,设C(﹣m,2m),m>0,tan∠A的值列出关于m的方程,解得m的值,则可得点C的坐标.
解:∵∠C=∠C,
∵OC2=BCAC,即![]() ,
,
∴△OBC∽△OAC,
∴∠A=∠COB,
∵α+∠COB=90°,∠A+∠ABO=90°,
∴∠ABO=α,
∵tanα=2,
∴tan∠ABO=![]() ,
,
∴OA=2OB,
∵AB=3![]() ,
,
由勾股定理可得:OA2+OB2=AB2,
即![]() ,
,
解得:OB=3,
∴OA=6,
∴tan∠A=![]() ,
,
如图,过点C作CD⊥x轴于点D,
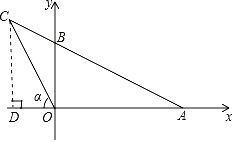
∵tanα=2,
∴设C(﹣m,2m),m>0,
∴AD=6+m,
∵tan∠A=![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:m=2,
经检验,m=2是原方程的解,
∴点C坐标为:(﹣2,4).
故选:A.

【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有2000名居民,试估计该小区居民一周内使用共享单车的总次数.
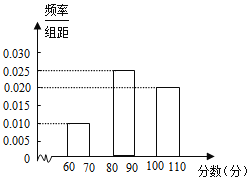
【题目】某社区为了加强居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与作答《2020年新型冠状病毒肺炎的防护全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从该社区抽取40名居民的答卷,并对他们的成绩(单位:分)进行整理、分析,过程如下:
收集数据
85 65 95 100 90 95 85 65 75 85 100 90 70 90 100 80 80 100 95 75 80 100 80 95 65 100 90 95 85 80 100 75 60 90 70 80 95 75 100 90
整理数据(每组数据可含最低值,不含最高值)
分组(分) | 频数 | 频率 |
60~70 | 4 | 0.1 |
70~80 | a | b |
80~90 | 10 | 0.25 |
90~100 | c | d |
100~110 | 8 | 0.2 |
分析数据
(1)填空:a= ,b= ,c= ,d= ;
(2)补全频率分布直方图;
(3)由此估计该社区居民在线答卷成绩在 (分)范围内的人数最多;
(4)如果该社区共有800人参与答卷,那么可估计该社区成绩在90分及以上约为 人.