题目内容
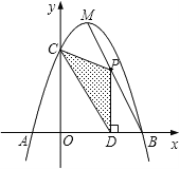
【题目】如图,AB为⊙O的直径,D是![]() 的中点,BC与AD,OD分别交于点E,F.
的中点,BC与AD,OD分别交于点E,F.
(1)求证:OD∥AC;
(2)求证:DC2=DEDA;
(3)若⊙O的直径AB=10,AC=6,求BF的长.

【答案】(1)见解析;(2)见解析;(3)4
【解析】
(1)由D是![]() 的中点,推出∠CAB=2∠BAD,再根据∠BOD=2∠BAD得∠CAB=∠BOD,故AC∥OD;
的中点,推出∠CAB=2∠BAD,再根据∠BOD=2∠BAD得∠CAB=∠BOD,故AC∥OD;
(2)证明△DCE∽△DCA,即可求解;
(3)根据△BOF∽△BAC,列出![]() =
=![]() ,求出BF=4.
,求出BF=4.
(1)因为点D是弧BC的中点,
所以∠CAD=∠BAD,即∠CAB=2∠BAD,
而∠BOD=2∠BAD,
所以∠CAB=∠BOD,
所以DO∥AC;
(2)∵D是![]() 的中点,
的中点,
∴∠CAD=∠DCB,
∴△DCE∽△DAC,
∴CD2=DEDA;
(3)∵AB为⊙O的直径
∴∠ACB=90°,
在Rt△ACB中,BC=.![]() =8,
=8,
∵OD∥AC,
∴△BOF∽△BAC,
∴![]() ,
,
即![]() =
=![]() ,
,
∴BF=4.
即BF的长为4.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目