题目内容
【题目】如图,![]() 是
是![]() 的外接圆,点
的外接圆,点![]() 在
在![]() 边上,
边上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .
.
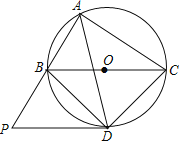
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]()
【答案】(1)见解析;(2)见解析
【解析】
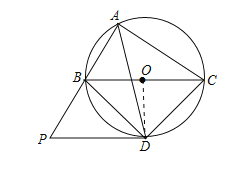
(1)由直径所对的圆周角为直角得到∠BAC为直角,再由AD为角平分线,得到一对角相等,根据同弧所对的圆心角等于圆周角的2倍及等量代换确定出∠DOC为直角,与平行线中的一条垂直,与另一条也垂直得到OD与PD垂直,即可得证;
(2)由PD与BC平行,得到一对同位角相等,再由同弧所对的圆周角相等及等量代换得到∠P=∠ACD,根据同角的补角相等得到一对角相等,利用两对角相等的三角形相似即可得证;
(1)∵圆心O在BC上,
∴BC是圆O的直径,
∴∠BAC=90°,
连接OD,
∵AD平分∠BAC,
∴∠BAC=2∠DAC,
∵∠DOC=2∠DAC,
∴∠DOC=∠BAC=90°,即OD⊥BC,
∵PD∥BC,
∴OD⊥PD,
∵OD为圆O的半径,
∴PD是圆O的切线;
(2)∵PD∥BC,
∴∠P=∠ABC,
∵∠ABC=∠ADC,
∴∠P=∠ADC,
∵∠PBD+∠ABD=180°,∠ACD+∠ABD=180°,
∴∠PBD=∠ACD,
∴△PBD∽△DCA.
![]() (相似三角形的对应边成比例)
(相似三角形的对应边成比例)
![]() .
.
![]() .
.
![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目