题目内容
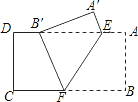
【题目】如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B'处，点A落在点A'处．
（1）求证：B'E＝BF；
（2）若AE＝1，B'E＝2，求梯形ABFE的面积．
【答案】（1）见解析；（2）
【解析】
（1）由折叠可得，BF＝
，依据
，可得B'F＝B'E，进而得到
；
（2）由折叠可得，
，
，根据勾股定理可得A'B'的长，再根据梯形面积计算公式，即可得到梯形ABFE的面积．
解：（1）由折叠可得，BF＝B'F，∠BFE＝∠B'FE，
由AD∥BC，可得∠B'EF＝∠BFE，
∴∠B'EF＝∠BFE，
∴B'F＝B'E，
∴B'E＝BF；
（2）由折叠可得，，，而B'E＝BF＝2，
∴A'B'＝
＝
＝
，
∴AB＝，
∴梯形ABFE的面积＝
＝
＝．
练习册系列答案
相关题目
