题目内容
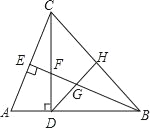
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连结DH、BE与相交于点G,以下结论中正确的结论有( )
(1)△ABC是等腰三角形;(2)BF=AC;(3)BH:BD:BC=1:![]() :
:![]() ;(4)GE2+CE2=BG2.
;(4)GE2+CE2=BG2.
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
(1)根据角平分线的定义可得∠ABE=∠CBE,根据等角的余角相等求出∠A=∠BCA,再根据等角对等边可得AB=BC,从而得证;
(2)根据三角形的内角和定理求出∠A=∠DFB,推出BD=DC,根据AAS证出△BDF≌△CDA即可;
(3)根据等腰直角三角形斜边上的中线等于斜边的一半进行解答;
(4)由(2)得出BF=AC,再由BF平分∠DBC和BE⊥AC通过ASA证得△ABE≌△CBE,即得CE=AE=![]() AC,连接CG,由H是BC边的中点和等腰直角三角形△DBC得出BG=CG,再由直角△CEG得出CG2=CE2+GE2,从而得出CE,GE,BG的关系.
AC,连接CG,由H是BC边的中点和等腰直角三角形△DBC得出BG=CG,再由直角△CEG得出CG2=CE2+GE2,从而得出CE,GE,BG的关系.
解:(1)∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵CD⊥AB,
∴∠ABE+∠A=90°,∠CBE+∠ACB=90°,
∴∠A=∠BCA,
∴AB=BC,
∴△ABC是等腰三角形;
故(1)正确;
(2)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°,
∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,
∴∠A=∠DFB,
∵∠ABC=45°,∠BDC=90°,
∴∠DCB=90°﹣45°=45°=∠DBC,
∴BD=DC,
在△BDF和△CDA中
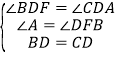 ,
,
∴△BDF≌△CDA(AAS),
∴BF=AC;
故(2)正确;
(3)∵在△BCD中,∠CDB=90°,∠DBC=45°,
∴∠DCB=45°,
∴BD=CD,BC=![]() BD.
BD.
由点H是BC的中点,
∴DH=BH=CH=![]() BC,
BC,
∴BD=![]() BH,
BH,
∴BH:BD:BC=BH:![]() BH:2BH=1:
BH:2BH=1:![]() :2.
:2.
故(3)错误;
(4)由(2)知:BF=AC,
∵BF平分∠DBC,
∴∠ABE=∠CBE,
又∵BE⊥AC,
∴∠AEB=∠CEB,
在△ABE与△CBE中,
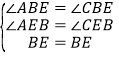 ,
,
∴△ABE≌△CBE(AAS),
∴CE=AE=![]() AC,
AC,
∴CE=![]() AC=
AC=![]() BF;
BF;
连接CG.
∵BD=CD,H是BC边的中点,
∴DH是BC的中垂线,
∴BG=CG,
在Rt△CGE中有:CG2=CE2+GE2,
∴CE2+GE2=BG2.
故(4)正确.
综上所述,正确的结论由3个.
故选:C.

 阅读快车系列答案
阅读快车系列答案