题目内容
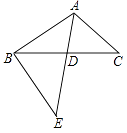
【题目】在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.
(1)依题意补全图1;
(2)如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;
(3)如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)
(4)如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.
【答案】
(1)解:如图1所示:
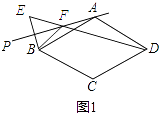
(2)解:∠ABF=∠ADF.
理由:如图2所示:连接AE.
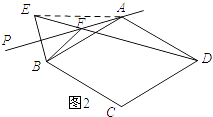
∵点B与点E关于直线PA对称,
∴EA=AB,∠ABF=∠AEF.
∵四边形ABCD为菱形,
∴AB=AD.
∴AE=AD.
∴∠AEF=∠ADF.
∴∠ABF=∠ADF.
(3)解:DF=ED﹣BF.
理由:如图3所示:
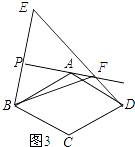
∵点B与点E关于PA对称,
∴EF=BF.
又∵DF=ED﹣EF,
∴DF=ED﹣BF.
(4)解:BF=DE+DF.
理由:如图4所示:
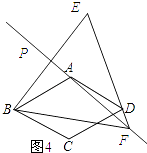
∵点B与点E关于PA对称,
∴EF=BF.
又∵EF=ED+DF,
∴BF=DE+DF
【解析】(1)根据题意画出图形;
(2)连接AE,根据对称的性质可得EA=AB、∠ABF=∠AEF,再由四边形ABCD为菱形,可得∠AEF=∠ADF,进而得出结论;
(3)根据对称的性质易得DF=ED﹣BF;
(4)画出图形,根据对称的性质易得BF=DE+DF.
【考点精析】根据题目的已知条件,利用菱形的性质和轴对称的性质的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.