��Ŀ����
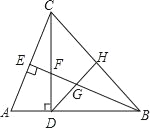
����Ŀ��̽���о�����֪����ABC�͡�CDE���ǵȱ������Σ�
��1����ͼ1������A��C��E��һ��ֱ����ʱ�����ǿ��Եõ����ۣ��߶�AD��BE��������ϵΪ���� �����߶�AD��BE���ɵ���Ƕ���Ϊ�� ���㣻
��2����ͼ2������A��C��E����һ��ֱ����ʱ����֤����1���еĽ�����Ȼ������
������ã�
��ͼ3��ij�㳡��һ���ı�������ABCD���ֲ�ã�AB��60m��BC��80m���ҡ�ABC��30�㣬��DAC����DCA��60�㣬����ˮ������B��D����֮��ľ��룮

���𰸡���1��AD=BE��60����2��֤������������3��ˮ������B��D����֮��ľ���Ϊ100m��
��������
������1�����ݵȱ������ε����ʿɵ�AC=BC��CD=CE����ACB=��DCE=60����Ȼ�������ACD=��BCE�����������߽DZ���֤����ACD����BCEȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AD=BE������ȫ�������ζ�Ӧ����ȿɵá�ADC=��BEC��Ȼ����������ε�һ����ǵ������������ڵ������ڽǵĺ������DPE=��DCE����2��֤����ACD�ա�BCE��SAS�����õ�AD=BE����DAC=��EBC�����ݡ�BPA=180��-��ABP-��BAP=180��-��ABC-��BAC�����ɽ�𣮣�3����ͼ3����ABΪ������ABC������ȱ���ABE������CE���ɣ�2���ɵã�BD=CE��֤����EBC��ֱ�������Σ����ù��ɶ������CE�ij��ȣ����ɽ��
�����������1���ߡ�ABC����CDE���ǵȱ������Σ�
��AC=BC��CD=CE����ACB=��DCE=60�㣬
���ACB+��BCD=��DCE+��BCD������ACD=��BCE��
����ACD����BCE��
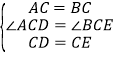 ��
��
���ACD�ա�BCE��SAS����
��AD=BE����ADC=��BEC��
�������ε�������ʣ���DPE=��PEA+��DAC����DCE=��ADC+��DAC��
���DPE=��DCE=60�㣻
�ʴ�Ϊ����ȣ�60��
��2���ߡ�ABC����CDE���ǵȱ������Σ�
��AC=BC��CD=CE����ACB=��DCE=60�㣬
���ACB+��BCD=��DCE+��BCD��
����ACD=��BCE��
����ACD����BCE��
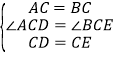 ��
��
���ACD�ա�BCE��SAS����
��AD=BE����DAC=��EBC��
���BPA=180�㩁��ABP����BAP=180�㩁��ABC����BAC=60��
��3����ͼ3����ABΪ������ABC������ȱ���ABE������CE��
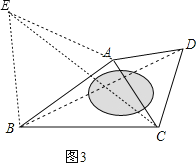
�ɣ�2���ɵã�BD=CE
���EBC=60��+30��=90�㣬
���EBC��ֱ��������
��EB=60m BC=80m��
��CE=![]() =100��m����
=100��m����
��ˮ������B��D����֮��ľ���Ϊ100m��

 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�