题目内容
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= ![]() 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.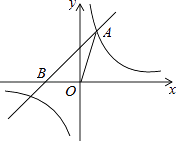
(1)求k和b的值;
(2)求△OAB的面积.
【答案】
(1)解:把A(2,5)分别代入y= ![]() 和y=x+b,
和y=x+b,
得 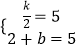 ,
,
解得k=10,b=3 。
(2)解:作AC⊥x轴于点C,
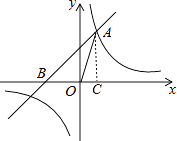
由(1)得直线AB的解析式为y=x+3,
∴点B的坐标为(﹣3,0),
∴OB=3,
∵点A的坐标是(2,5),
∴AC=5,
∴ ![]() =
= ![]() 5=
5= ![]() .
.
【解析】(1)(1)根据已知可知点A事两函数图像的交点,因此将点A的坐标分别代入两函数解析式,建立方程,即可求出k和b的值。
(2)要求△OAB的面积,根据已知可知必须求出点B的坐标,根据直线AB与x轴交点为B,根据y=0建立方程求解,得出点B的坐标,再根据三角形的面积公式求解即可。

练习册系列答案
相关题目