��Ŀ����
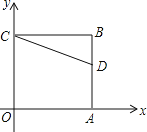
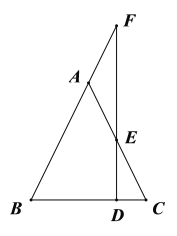
����Ŀ����ͼ1������ȫ�ȵġ�ABC�͡�DEF�У���ACB=��DFE=90�㣬AB=DE�����е�B�͵�D�غϣ���F��BC�ϣ�����DEF������BCƽ�ƣ���ƽ�Ƶľ���Ϊx��ƽ�ƺ��ͼ�����ABC�غϲ��ֵ����Ϊy��y����x�ĺ���ͼ����ͼ2��ʾ������0��x��m��m��x��3��3��x��4ʱ�������Ľ���ʽ��ͬ��
��1����գ�BC�ij�Ϊ_____��
��2����y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��

���𰸡���1��4����2��y= .
.
�����������������
��1�����ͼ1��ͼ2������֪����x=4ʱ��y=0��˵����ʱ����B�˶����˵�C�������������ص����֣��Ӷ��ɵ�BC=4��
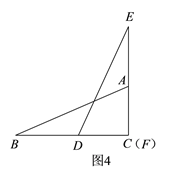
��2������ͼ1��ͼ2�е���Ϣ��֪����DE������Aʱ����ͼ3����BD=x=3��CD=1��ͨ��֤��ADC�ס�BAC�����AC=2=DF������ͼ1��ͼ2��֪����F���C�غ�ʱ����ͼ4����BD=x=m=BC-DF=4-2=2�������ɵã����κ�����Ӧ���Ա�����ȡֵ��Χ�ֱ��ǣ���![]() ����
����![]() ����
����![]() �������������Ա�����ȡֵ��Χ����ͼ5����6��ͼ7�����֪��������������ö�Ӧ�ĺ�����ϵʽ������ۺϼ���.
�������������Ա�����ȡֵ��Χ����ͼ5����6��ͼ7�����֪��������������ö�Ӧ�ĺ�����ϵʽ������ۺϼ���.
���������
��1����ͼ2�õ�x=4ʱ��y=0��˵����ʱ��DEF����ABC���غϲ��֣�
���D��B��C�˶��ľ���Ϊ4����BC=4��
��2����ͼ3����DE������Aʱ����ͼ2�е���Ϣ��֪����ʱBD=x=3��CD=BC-BD=1��
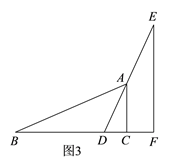
�ߡ�ABC�ա�DEF��
���EDF=��BAC��
�ߡ�ACD=��BCA
���ADC�ס�BAC��
��![]() ����
����![]() ����ã�AC=2��
����ã�AC=2��
��DF=AC=2.
����ͼ1��ͼ2��֪����F���C�غ�ʱ����ͼ4����BD=x=m=BC-DF=4-2=2.
�����κ�����Ӧ���Ա�����ȡֵ��Χ�ֱ��ǣ���![]() ����
����![]() ����
����![]() ��
��
�ٵ�0��x��2ʱ����ͼ5����
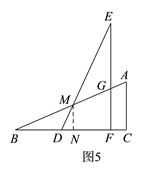
��ED��EF��AB�ֱ��ཻ�ڵ�M��G����MN��BC������ΪN��
����MNB=90��=��EFD=��C��
�ߡ�MDN=��EDF��
���DMN�ס�DEF��
��![]() ����
����![]() ��
��
��MN=2DN��
��DN=n����MN=2n��
ͬ����BMN�ס�BAC��
��![]() ����
����![]() ��
��
��BN=4n����x+n=4n��
��n=![]() x��
x��
��S��BDM=![]() BDMN=
BDMN=![]()
ͬ����BGF�ס�BAC
��![]() ����
����![]() ��
��
��GF=![]() (x+2)��
(x+2)��
��y=S��BGF��S��BDM=![]() ��x+2����
��x+2����![]() ��x+2��-
��x+2��-![]() =��
=��![]() x2+x+1��
x2+x+1��
�ڵ�2��x��3ʱ����ͼ6����
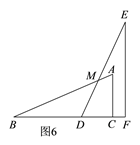
�ɢ�֪��S��BDM=![]() x2��
x2��
��y=S��ABC��S��BDM=![]() ��2��4-
��2��4-![]() x2=��
x2=��![]() x2+4
x2+4
�۵�3��x��4ʱ����ͼ7����
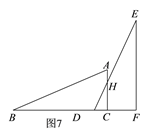
��DE��AB�ཻ�ڵ�H��������DHC�ס�DEF��
��![]() ����
����![]()
��HC=24��x��
��y=![]() =x2��8x+16��
=x2��8x+16��
�����������ɵ�y����x�ĺ�����ϵʽΪ��
y= ��
��

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�