题目内容
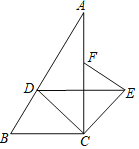
【题目】已知如图,等腰梯形ABCD,AB=CD,BE=CE,求证:AE=DE.

【答案】见解析
【解析】【试题分析】
等腰梯形ABCD,AB=CD,根据等腰梯形的性质得:∠ABC=∠DCB,因为BE=CE,根据等边对等角得:∠EBC=∠ECB;根据等式的性质得:∠EBC﹣∠ABC=∠ECB﹣∠DCB,即∠EBA=∠ECD;在△EBA和△ECD中,AB=CD,∠EBA=∠ECD,BE=CE,根据边角边定理得:△EBA≌△ECD(SAS),根据全等三角形的性质得:AE=DE.
【试题解析】
∵等腰梯形ABCD,AB=CD,
∴∠ABC=∠DCB,
∵BE=CE,
∴∠EBC=∠ECB,
∴∠EBC﹣∠ABC=∠ECB﹣∠DCB,
即∠EBA=∠ECD,
在△EBA和△ECD中,
AB=CD,∠EBA=∠ECD,BE=CE,
∴△EBA≌△ECD(SAS),
∴AE=DE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目