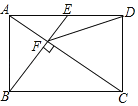
题目内容
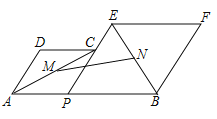
【题目】如图,已知![]() ,
,![]() 为线段
为线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() ,
,![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() .点
.点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() ,
,![]() 、
、![]() 分别是对角线
分别是对角线![]() 、
、![]() 的中点.当点
的中点.当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 、
、![]() 之间的距离最短为_______.
之间的距离最短为_______.
【答案】![]()
【解析】
连接PM、PN,根据菱形的性质求出∠CAP=![]() 30°,∠MPC=
30°,∠MPC=![]() ∠CPA=60°,∠EPN=∠BPN=
∠CPA=60°,∠EPN=∠BPN=![]() ∠EPB=30°,从而求出∠MPN=90°,设AP=x,则PB=2a-x,然后利用锐角三角函数求出PM和PN,然后利用勾股定理求出MN2与x的函数关系式,化为顶点式即可求出MN2的最小值,从而求出结论.
∠EPB=30°,从而求出∠MPN=90°,设AP=x,则PB=2a-x,然后利用锐角三角函数求出PM和PN,然后利用勾股定理求出MN2与x的函数关系式,化为顶点式即可求出MN2的最小值,从而求出结论.
解:连接PM、PN

∵四边形![]() 和四边形
和四边形![]() 为菱形,
为菱形,![]()
∴∠CPA=180°-∠DAP=120°,∠EPB=∠DAP=60°,PM⊥AC,PN⊥EB,AC平分∠DAP,PM平分∠APC,PN平分∠EPB
∴∠CAP=![]() 30°,∠MPC=
30°,∠MPC=![]() ∠CPA=60°,∠EPN=∠BPN=
∠CPA=60°,∠EPN=∠BPN=![]() ∠EPB=30°
∠EPB=30°
∴∠MPN=∠MPC+∠EPN=90°
设AP=x,则PB=2a-x
∴PM=AP·sin∠CAP=![]() ,PN=PB·cos∠BPN=
,PN=PB·cos∠BPN=![]() (2a-x)
(2a-x)
在Rt△MON中
MN2= PM2+PN2=![]() +
+![]() (2a-x)2=(x-
(2a-x)2=(x-![]() a)2+
a)2+![]() a2
a2
当x=![]() a时,MN2取最小值,最小为
a时,MN2取最小值,最小为![]() a2
a2
∴MN的最小值为![]()
故答案为:![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目