题目内容
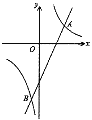
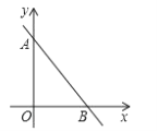
【题目】如图,在直角坐标系xOy中,O为坐标原点,直线AB分别与y轴,x轴交于A(0,4),B(3,0)两点.
(1)尺规作图:在x轴上求作一点C,使得△ABC是以![]() 为顶角的等腰三角形,并在图中标明相应字母;(保留作图痕迹,不写作法)
为顶角的等腰三角形,并在图中标明相应字母;(保留作图痕迹,不写作法)
(2)在(1)的条件下,求点C的坐标.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用尺规作图作线段AB的中垂线,与x轴的交点即为点C,连接AC、BC即可得;
(2)设OC=x,利用勾股定理得出AC2=OA2+OC2=42+x2,BC2=(OC2+OB2)=(x+3)2,依据AC=BC得出关于x的方程,解之可得.
(1)如图所示,△ABC即为所求.

(2)设OC=x,
∵A(0,4),B(3,0),
∴OA=4,OB=3,
∴AC2=OA2+OC2=42+x2,BC2=(OC2+OB2)=(x+3)2,
∴42+x2=(x+3)2,
解得x=![]() ,
,
∴C(﹣![]() ,0).
,0).

【题目】学校运动会的立定跳远和1分钟跳绳两个单项比赛分成预赛和决赛两个阶段.下表为参加这两项比赛的10名学生的预赛成绩:
学生编号 成绩 项目 | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1分钟跳绳(单位:次) | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
在这10名学生中,同时进入两项决赛的只有6人,进入立定跳远决赛的有8![]() 的值是__________.
的值是__________.
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?