Question

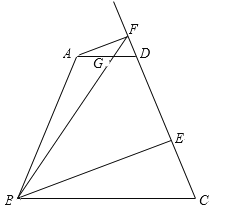
【题目】如图，点E是矩形ABCD的边AD的中点，且BE⊥AC于点F，则下列结论中错误的是（ ）

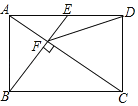
A.AF＝CF

B.∠DCF＝∠DFC

C.图中与△AEF相似的三角形共有5个

D.tan∠CAD＝

Answer 1

【答案】D

【解析】

由AE=AD=BC，又AD∥BC，所以，故A正确，不符合题意；

过D作DM∥BE交AC于N，得到四边形BMDE是平行四边形，求出BM=DE=BC，得到CN=NF，根据线段的垂直平分线的性质可得结论，故B正确，不符合题意；

根据相似三角形的判定即可求解，故C正确，不符合题意；

由△BAE∽△ADC，得到CD与AD的大小关系，根据正切函数可求tan∠CAD的值，故D错误，符合题意．

解：A、∵AD∥BC，

∴△AEF∽△CBF，

∴＝，

∵AE＝AD＝BC，

∴＝，故A正确，不符合题意；

B、过D作DM∥BE交AC于N，

∵DE∥BM，BE∥DM，

∴四边形BMDE是平行四边形，

∴BM＝DE＝BC，

∴BM＝CM，

∴CN＝NF，

∵BE⊥AC于点F，DM∥BE，

∴DN⊥CF，

∴DF＝DC，

∴∠DCF＝∠DFC，故B正确，不符合题意；

C、图中与△AEF相似的三角形有△ACD，△BAF，△CBF，△CAB，△ABE共有5个，故C正确，不符合题意．

D、设AD＝a，AB＝b由△BAE∽△ADC，有＝．

∵tan∠CAD＝＝＝，故D错误，符合题意．

故选：D．