题目内容
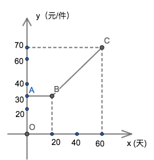
【题目】某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第 x 天的成本 y(元/件)与 x(天)之间的关系如图所示,并连续 60 天均以 80 元/件的价格出售, 第 x 天该产品的销售量 z(件)与 x(天)满足关系式 z=x+15.
(1)第 25 天,该商家的成本是 元,获得的利润是 元;
(2)设第 x 天该商家出售该产品的利润为 w 元.
①求 w 与 x 之间的函数关系式;
②求出第几天的利润最大,最大利润是多少?
【答案】(1)35,1800;(2)①![]() ;②第27或28天的利润最大,最大为1806元.
;②第27或28天的利润最大,最大为1806元.
【解析】
(1)根据已知条件可知第25天时的成本为35元,此时的销售量为40,则可求得第25天的利润.
(2)①利用每件利润×总销量=总利润,分当0<x≤20时与20<x≤60时,分别列出函数关系式;
②利用一次函数及二次函数的性质即可解答.
解:(1)由图象可知,此时的销售量为z=25+15=40(件),
设直线BC的关系为y=kx+b,将B(20,30)、C(60,70)代入
得:![]() ,解得:k=1,b=10,
,解得:k=1,b=10,
∴y=x+10,
∴第 25 天,该商家的成本是y=25+10=35(元)
则第25天的利润为:(8035)×40=1800(元);
故答案为:35,1800;
(2)①当0<x≤20时,![]() ;
;
当20<x≤60时,![]() ,
,
∴ ![]()
②当0<x≤20时,∵50>0,w随x的增大而增大,
∴当x=20时,w=50×20+750=1750(元),
当20<x≤60时,![]() ,
,
∵-1<0,抛物线开口向下,对称轴为![]() ,
,
当x=27与x=28时,![]() (元)
(元)
∵1806>1750,
∴第27或28天的利润最大,最大为1806元.

练习册系列答案
相关题目