��Ŀ����
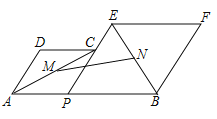
����Ŀ����ͼ����֪�����߾�y��ax2+bx��3��A��1��0����B��3��0����C���㣮

��1���������߽���ʽ��
��2����ͼ1����P��BC�Ϸ���������һ�㣬��PQ��y�ύBC��Q�㣮�����Ƿ���ڵ�Pʹ�á�BPQΪ���������Σ������ڣ���ֱ��д��P�����ꣻ�������ڣ���˵�����ɣ�
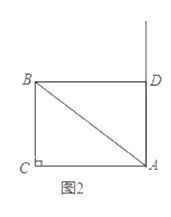
��3����ͼ2������AC����D���߶�AB��һ�㣬��DE��BC��AC��E�㣬����BE������BDE�ס�CEB����D�����꣮
���𰸡���1��y����x2+4x��3����2�����ڵ�Pʹ�á�BPQΪ���������Σ�P������ΪP1��1��0����P2��2��1����![]() ����3��
����3��![]() .
.
��������
��1�����ô���ϵ�������ɵ������ߵı���ʽ��
��2�������ֱ��![]() �Ľ���ʽ���������������
�Ľ���ʽ���������������![]() ʱ����
ʱ����![]() ���ɱ�ʾ�������߶γ�����ⷽ�̿����P�����ꣻ
���ɱ�ʾ�������߶γ�����ⷽ�̿����P�����ꣻ
��3��֤��![]() �ɵñ����߶����AE������
�ɵñ����߶����AE������![]() ʱ�����D�����꣮
ʱ�����D�����꣮
��1����![]() ����
����![]() �ã�
�ã�![]() ��
��
���![]() ��
��
�����߽���ʽ![]() ��
��
��2�����ڵ�Pʹ�á�BPQΪ���������Σ�
��B��3��0����C��0����3����
����ֱ��BC�Ľ���ʽΪ![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��ֱ��BC�Ľ���ʽΪ![]() ��
��
��![]() ����
����![]() ���ɷ�����������ǣ�
���ɷ�����������ǣ�
�ٵ�![]() ʱ���������P��Q����x��Գƣ�
ʱ���������P��Q����x��Գƣ�
��![]() ��
��
��ã�![]() ����ȥ����
����ȥ����
��![]() ��
��
�ڵ�![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ����ȥ����
����ȥ����![]() ��
��
��![]() ��
��
�۵�![]() ʱ����
ʱ����![]() ��
��
�����ã�![]() ��
��
���![]() ��
��
��![]() ��
��
�ۺ����Ͽɵ�P������ΪP1��1��0����P2��2��1����![]() ��
��
��3���ߡ�BDE�ס�CEB��
���ABE����ACB��
�ߡ�BAE����CAB��
���ABE�ס�ACB��
�֡�![]() ��
��
��![]()
��![]()
��![]()
��![]() ��
��
��![]()
��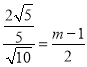
��![]()
��![]() .
.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ѧУ�˶����������Զ��1���������������������ֳ�Ԥ���;��������Σ��±�Ϊ�μ������������10��ѧ����Ԥ���ɼ���
ѧ����� �ɼ� ��Ŀ | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
������Զ����λ���ף� | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1��������������� | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
����10��ѧ���У�ͬʱ�������������ֻ��6�ˣ�����������Զ��������8![]() ��ֵ��__________��
��ֵ��__________��
����Ŀ��������������ͬ�����������10�����ѵ�������˵ijɼ���ͼ��ʾ��

����������Ϣ�����������������£�
ƽ���ɼ�/�� | ��λ��/�� | ����/�� | |
�� | ______ | 7 | 1.2 |
�� | 7 | ______ | ______ |
��1����ɱ���
��2������ѵ���ɼ�������Ϊѡ����һ����Ա�������ã�Ϊʲô��