��Ŀ����
����Ŀ��ij��ѧ�˶����ж��ܡ����ܡ���Զ��ʵ�����ĸ�ѵ��С�ӣ��ֽ��ĸ�ѵ��С�Ӷ�Ա������Ƴ����²�������ͳ��ͼ:
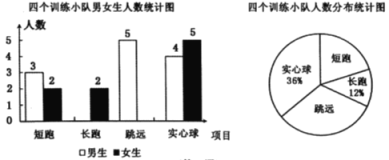
(l)ѧУ�˶��ӵĶ�Ա������Ϊ �ˣ�����ͳ��ͼ�ж���ѵ��С������ӦԲ�ĽǵĶ���Ϊ ;
(2)��ȫ����ͳ��ͼ������������;
(3)���ڶ���ѵ��С�������ѡȡ2��ͬѧ���б����������оٷ�(����״ͼ���б�)����ѡȡ��������ͬѧǡ����һ��һŮ�ĸ���.
���𰸡���1��25.72����2����������1�ˣ���ԶŮ��3�ˣ���3��![]() .
.
��������
��1����������5+4����36%=25���ˣ���Բ�Ľǣ�![]() ����2�����б��������.
����2������������.
�⣺��1����������5+4����36%=25���ˣ���Բ�Ľǣ�![]()
��2���б�
��1 | ��2 | ��3 | Ů1 | Ů2 | ||||||
��1 | ��1 | ��2 | ��1 | ��3 | ��1 | Ů1 | ��1 | Ů2 | ||
��2 | ��2 | ��1 | ��2 | ��3 | ��2 | Ů1 | ��2 | Ů2 | ||
��3 | ��3 | ��1 | ��3 | ��2 | ��3 | Ů1 | ��3 | Ů2 | ||
Ů1 | Ů1 | ��1 | Ů1 | ��2 | Ů1 | ��3 | Ů1 | Ů2 | ||
Ů2 | Ů2 | ��1 | Ů2 | ��2 | Ů2 | ��3 | Ů2 | Ů1 | ||
���ԣ�P��ǡ��һ��һŮ��=![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij�̳���Ϊ�������˿ͣ�������ɫ���˽�������ٰ�����Ʒ�н���������������200Ԫ�ߣ������ֽ���������ѡ��һ��ֱ�ӻ��20Ԫ�����ȯ�����ǵõ�һ��ҡ���Ļ��ᣮ��֪��ҡ������װ��2�������2��������ɫ����������ͬ��ҡ���߱����ҡ������һ������ҡ���������������ɫ����������������ȯ�Ķ��٣�
�� | ���� | һ��һ�� | ���� |
���ȯ��Ԫ�� | 18 | 24 | 18 |
��1���������б���������״ͼ������һ������ҡ��һ��һ������ĸ��ʣ�
��2�����һ���˿͵����ڱ��깺����200Ԫ����ֻ���ǻ��������Ʒȯ�������������ѡ�����ַ�����Ϊʵ�ݣ�