题目内容
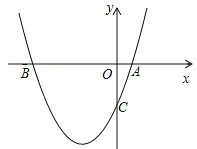
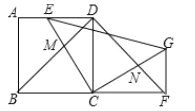
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是
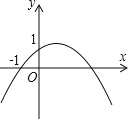
A.5个 B.4个 C.3个 D.2个
【答案】B
【解析】
∵二次函数y=ax2+bx+c(a≠0)过点(0,1)和(﹣1,0),∴c=1,a﹣b+c=0。
①∵抛物线的对称轴在y轴右侧,∴![]() x>0。∴a与b异号。∴ab<0,正确。
x>0。∴a与b异号。∴ab<0,正确。
②∵抛物线与x轴有两个不同的交点,∴b2﹣4ac>0。
∵c=1,∴b2﹣4a>0,即b2>4a。正确。
④∵抛物线开口向下,∴a<0。
∵ab<0,∴b>0。
∵a﹣b+c=0,c=1,∴a=b﹣1。∴b﹣1<0,即b<1。∴0<b<1,正确。
③∵a﹣b+c=0,∴a+c=b。∴a+b+c=2b>0。
∵b<1,c=1,a<0,∴a+b+c=a+b+1<a+1+1=a+2<0+2=2。∴0<a+b+c<2,正确。
⑤抛物线y=ax2+bx+c与x轴的一个交点为(﹣1,0),设另一个交点为(x0,0),则x0>0,
由图可知,当﹣1<x<x0时,y>0;当x>x0时,y<0。
∴当x>﹣1时,y>0的结论错误。
综上所述,正确的结论有①②③④。故选B。

 每日10分钟口算心算速算天天练系列答案
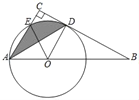
每日10分钟口算心算速算天天练系列答案【题目】如图,点P是弧AB所对弦AB上一动点,过点P作PC⊥AB交AB于点P,作射线AC交弧AB于点D.已知AB=6cm,PC=1cm,设A,P两点间的距离为xcm,A,D两点间的距离为ycm.(当点P与点A重合时,y的值为0)
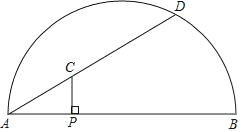
小平根据学习函数的经验,分别对函数y随自变量x的变化而变化的规律进行了探究.
下面是小平的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 4.24 | 5.37 | m | 5.82 | 5.88 | 5.92 |
经测量m的值是 (保留一位小数).
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y),并画出函数y的图象;

(3)结合函数图象,解决问题:当∠PAC=30°,AD的长度约为 cm.
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.