题目内容
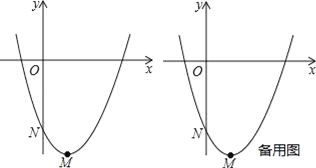
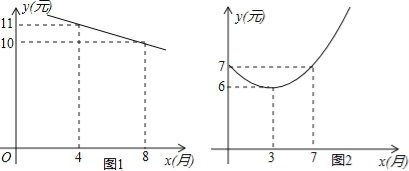
【题目】某水果店销售某中水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)的变化趋势,每千克成本y2(元)与销售时间第x月满足函数关系式y2=mx2﹣8mx+n,其变化趋势如图2.
(1)求y2的解析式;
(2)第几月销售这种水果,每千克所获得利润最大?最大利润是多少?
【答案】(1) y2=![]() x2﹣x+
x2﹣x+![]() (1≤x≤12);(2) 第3月销售这种水果,每千克所获得利润最大,最大利润是
(1≤x≤12);(2) 第3月销售这种水果,每千克所获得利润最大,最大利润是![]() 元/千克.
元/千克.
【解析】
试题(1)把函数图象经过的点(3,6),(7,7)代入函数解析式,解方程组求出m、n的值,即可得解;
(2)根据图1求出每千克的售价y1与x的函数关系式,然后根据利润=售价﹣成本得到利润与x的函数关系式,然后整理成顶点式形式,再根据二次函数的最值问题解答即可.
试题解析:(1)由图可知,y2=mx2﹣8mx+n经过点(3,6),(7,7),
∴![]() ,
,
解得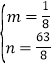 .
.
∴y2=![]() x2﹣x+
x2﹣x+![]() (1≤x≤12);
(1≤x≤12);
(2)设y1=kx+b(k≠0),
由图可知,函数图象经过点(4,11),(8,10),
则![]() ,
,
解得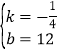 ,
,
所以,y1=﹣![]() x+12,
x+12,
所以,每千克所获得利润=(﹣![]() x+12)﹣(
x+12)﹣(![]() x2﹣x+
x2﹣x+![]()
![]() )
)
=﹣![]() x+12﹣
x+12﹣![]() x2+x﹣
x2+x﹣![]()
=﹣![]() x2+
x2+![]() x+
x+![]()
=﹣![]() (x2﹣6x+9)+
(x2﹣6x+9)+![]() +
+![]()
=﹣![]() (x﹣3)2+
(x﹣3)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当x=3时,所获得利润最大,为![]() 元.
元.
答:第3月销售这种水果,每千克所获得利润最大,最大利润是![]() 元/千克.
元/千克.

【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?