题目内容
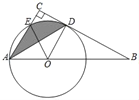
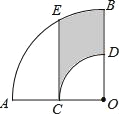
【题目】如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交
于点E，以点O为圆心，OC的长为半径作
交OB于点D．若OA=4，则图中阴影部分的面积为（ ）
A. 
+
B. +2 C. +
D. 2+
【答案】B
【解析】
连接OE、AE，根据点C为OC的中点可得∠CEO=30°，继而可得△AEO为等边三角形，求出扇形AOE的面积，最后用扇形AOB的面积减去扇形COD的面积，再减去S空白AEC即可求出阴影部分的面积．
解：连接OE、AE，
∵点C为OA的中点，
∴EO=2OC，
∴∠CEO=30°，∠EOC=60°，
∴△AEO为等边三角形，
∴S扇形AOE=
=
，
∴S阴影=S扇形AOB﹣S扇形COD﹣（S扇形AOE﹣S△COE）
=
﹣
﹣（﹣
）
=4π﹣π﹣+2
=
+2
故选：B．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
【题目】已知二次函数
，
与
的部分对应值如下表所示：
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断：
①抛物线的顶点为
；
②
；
③关于的方程
的解为
；
④
．
其中，正确的有___________________．
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如下表：
碟子的个数 | 碟子的高度（单位：cm） |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |
（1）当桌子上放有x（个）碟子时，请写出此时碟子的高度（用含x的式子表示）；
（2）分别从三个方向上看，其三视图如上图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度．
