ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżÄłÌćÓęÀÏÊŠËæ»úłéÈĄÁËŸĆÄꌶŒŚĄąÒÒÁœ°àČż·ÖѧÉúœűĐĐÒ»·ÖÖÓÌűÉț”ÄČâÊÔŁŹČą¶ÔłÉŒšœűĐĐÍłŒÆ·ÖÎöŁŹ»æÖÆÁËÆ”Êę·ÖČŒ±íșÍÍłŒÆÍŒŁŹÇëÄăžùŸĘÍŒ±íÖĐ”ÄĐĆÏąÍêłÉÏÂÁĐÎÊÌâŁș
·ÖŚé | Æ”Êę | Æ”ÂÊ |
”ÚÒ»Śé(0ĄÜx<120) | 3 | 0.15 |
”Ú¶țŚé(120ĄÜx<160) | 8 | a |
”ÚÈęŚé(160ĄÜx<200) | 7 | 0.35 |
”ÚËÄŚé(200ĄÜx<240) | b | 0.1 |
(1)Æ”Êę·ÖČŒ±íÖĐaŁœ____ŁŹbŁœ_____ŁŹČąœ«ÍłŒÆÍŒČčłäÍêŐûŁ»
(2)ÈçčûžĂĐŁŸĆÄꌶčČÓĐѧÉú360ÈËŁŹčÀŒÆÌűÉțÄÜč»Ò»·ÖÖÓÍêłÉ160»ò160ŽÎÒÔÉÏ”ÄѧÉúÓжàÉÙÈËŁż
(3)ÒŃÖȘ”ÚÒ»ŚéÖĐÓĐÁœžöŒŚ°àѧÉúŁŹ”ÚËÄŚéÖĐÖ»ÓĐÒ»žöŒŚ°àѧÉúŁŹÀÏÊŠËæ»úŽÓŐâÁœžöŚéÖĐžśŃĄÒ»ĂûѧÉúÌžČâÊÔÌć»áŁŹÔòËùŃĄÁœÈËŐęșöŒÊÇŒŚ°àѧÉú”ÄžĆÂÊÊǶàÉÙŁż

ĄŸŽđ°žĄż(1)0.4ŁŹ2Ł»ČčÍŒŒûœâÎöŁ»(2)162ÈËŁ»(3)![]() .
.
ĄŸœâÎöĄż
(1)ÓÉÍłŒÆÍŒÒŚ”ĂaÓëb”ÄÖ”ŁŹŒÌ¶űœ«ÍłŒÆÍŒČčłäÍêŐûŁ»
(2)ÀûÓĂÓĂŃù±ŸčÀŒÆŚÜÌć”ÄÖȘʶÇóœâŒŽżÉÇó”Î𰞣»
(3)ÊŚÏÈžùŸĘÌâÒ⻳öÊśŚŽÍŒŁŹÈ»șóÓÉÊśŚŽÍŒÇó”ĂËùÓĐ”ÈżÉÄܔĜáčûÓëËùŃĄÁœÈËŐęșöŒÊÇŒŚ°àѧÉú”ÄÇéżöŁŹÔÙÀûÓĂžĆÂÊč«ÊœŒŽżÉÇó”Î𰞣ź
œâŁș(1)aŁœ1©0.15©0.35©0.1Łœ0.4Ł»
ĄßŚÜÈËÊęÎȘŁș3ĄÂ0.15Łœ20(ÈË)ŁŹ
ĄàbŁœ20ĄÁ0.1Łœ2(ÈË)Ł»
čÊŽđ°žÎȘŁș0.4ŁŹ2Ł»
ČčÈ«ÍłŒÆÍŒ”ĂŁș
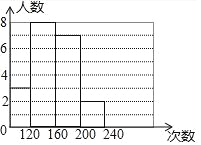
(2)žùŸĘÌâÒâ”ĂŁș
360ĄÁ(0.35+0.1)Łœ162(ÈË)ŁŹ
ŽđŁșÌűÉțÄÜč»Ò»·ÖÖÓÍêłÉ160»ò160ŽÎÒÔÉÏ”ÄѧÉúÓĐ162ÈËŁ»
(3)žùŸĘÌâÒâ»ÊśŚŽÍŒÈçÏÂŁș
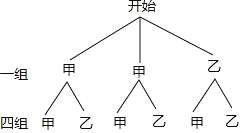
ĄßčČÓĐ6ÖÖ”ÈżÉÄܔĜáčûŁŹËùŃĄÁœÈËŐęșöŒÊÇŒŚ°àѧÉú”ÄÓĐ2ÖÖÇéżöŁŹ
ĄàËùŃĄÁœÈËŐęșöŒÊÇŒŚ°àѧÉú”ÄžĆÂÊÊÇŁș![]() Łœ
Łœ![]() Łź
Łź