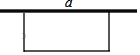题目内容
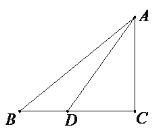
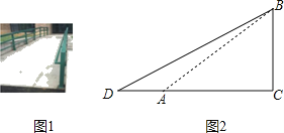
【题目】图1是无障碍通道，图2是其截面示意图，已知坡角∠BAC=30°，斜坡AB=4m，∠ACB=90°．现要对坡面进行改造，使改造后的坡角∠BDC=26.5°，需要把水平宽度AC增加多少m（结果精确到0.1）？（参考数据：
≈1.73，sin26.5°≈0.45，cos26.5°≈0.90，tan26.5°≈0.50）
【答案】需要把水平宽度约增加0.5米
【解析】
根据正弦的定义求出BC，根据余弦的定义求出AC，利用正切的定义求出DC，结合图形计算，进而得到答案．
解：在Rt△ABC中，∠BAC=30°，AB=4，
∴BC=ABsin30°=2，AC=ABcos30°=2
，
在Rt△DBC中，∠BDC=26.5°，tan∠BDC=
，
∴DC=
=
，
∴DA=-2≈4-3.46≈0.5（m），
答：需要把水平宽度约增加0.5米．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试，并对成绩进行统计分析，绘制了频数分布表和统计图，请你根据图表中的信息完成下列问题：
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
(1)频数分布表中a＝____，b＝_____，并将统计图补充完整；
(2)如果该校九年级共有学生360人，估计跳绳能够一分钟完成160或160次以上的学生有多少人？
(3)已知第一组中有两个甲班学生，第四组中只有一个甲班学生，老师随机从这两个组中各选一名学生谈测试体会，则所选两人正好都是甲班学生的概率是多少？
