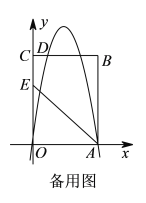题目内容
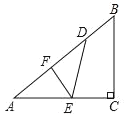
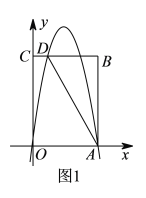
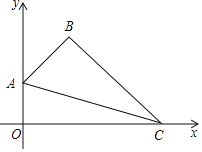
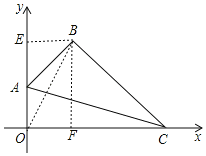
【题目】如图,在平面直角坐标系中,四边形OABC的顶点A的坐标为(0,1),点B的坐标为(1,2),∠ABC=90°,连接AC.
(1)求直线AC的函数表达式;
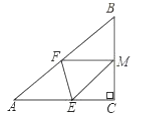
(2)点P是线段OC上一动点,从点O向点C运动,过点P作PM∥y轴,分别交AB或BC,AC于点M,N,其中点P的横坐标为m,MN的长为n.
①当0<m≤1时,求n与m之间的函数关系式;
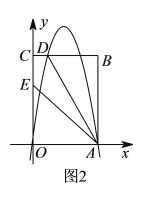
②当△AMN的面积最大时,请直接写出m的值.
【答案】(1)y=﹣![]() x+1;(2)①n=
x+1;(2)①n=![]() m;②m=
m;②m=![]() 时,△AMN的面积最大为
时,△AMN的面积最大为![]()
【解析】
(1)先求出点C坐标,再利用待定系数法可求解析式;
(2)①先求出直线AB,BC的解析式,分别表示M,N两点坐标,即可求解;
②分点M在AB上,点M在BC上两种情况讨论,利用一次函数的性质和二次函数的性质分别求出面积最大值,即可求解.
解:(1)如图,过点B作BE⊥y轴于点E,作BF⊥OC于点F,连接OB,
∵点A的坐标为(0,1),点B的坐标为(1,2),
∴OA=1,BE=OF=1,BF=OE=2,
∴AE=BE=1,
∴∠EAB=45°,
∴∠BAO=135°,
∵∠OAB+∠AOC+∠ABC+∠BCO=360°,
∴∠BCO=45°,
∴∠BCO=∠CBF=45°,
∴BF=CF=2,
∴OC=3,
∴点C(3,0),
设直线AC解析式为:y=kx+1,
∴0=3k+1,
∴k=﹣![]() ,
,
∴直线AC解析式为:y=﹣![]() x+1;
x+1;
(2)①如图,∵A的坐标为(0,1),点B的坐标为(1,2),点C坐标(3,0)
易得直线AB解析式为:y=x+1,直线BC解析式为:y=﹣x+3,
当0<m≤1时,即点M在AB上,
∵点P的横坐标为m,
∴点M(m,m+1),点N(m,﹣![]() m+1),
m+1),
∴MN=n=(m+1)﹣(﹣![]() m+1)=
m+1)=![]() m;
m;
②当0<m≤1时,MN=n=![]() m,
m,
∴S△AMN=![]() ×m×
×m×![]() m=
m=![]() m2,
m2,
∴当m=1时,△AMN的面积最大为![]() ,
,
当1<m≤3时,同①可得:M'N'=n=﹣m+3﹣(﹣![]() m+1)=﹣
m+1)=﹣![]() m+2,
m+2,
∴S△AMN=![]() ×m×(﹣
×m×(﹣![]() m+2)=﹣
m+2)=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∴当m=![]() 时,△AMN的面积最大为
时,△AMN的面积最大为![]() ,
,
综上所述:当m=![]() 时,△AMN的面积最大为
时,△AMN的面积最大为![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
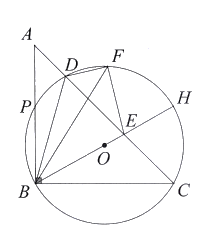
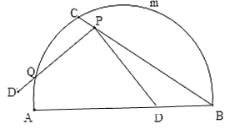
优秀生应用题卡口算天天练系列答案【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
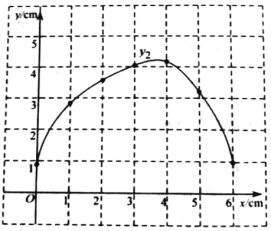
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)
【题目】某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
(1)频数分布表中a=____,b=_____,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计跳绳能够一分钟完成160或160次以上的学生有多少人?
(3)已知第一组中有两个甲班学生,第四组中只有一个甲班学生,老师随机从这两个组中各选一名学生谈测试体会,则所选两人正好都是甲班学生的概率是多少?