题目内容
【题目】已知二次函数![]() (
(![]() ).
).
(1)求出二次函数图象的对称轴;
(2)若该二次函数的图象经过点![]() ,且整数
,且整数![]() ,
,![]() 满足
满足![]() ,求二次函数的表达式;
,求二次函数的表达式;
(3)对于该二次函数图象上的两点![]() ,
,![]() ,设
,设![]() ,当
,当![]() 时,均有
时,均有![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)x=2;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)二次函数图象的对称轴是![]() ;
;
(2)代入![]() 点,求出a,b之间的关系,分情况讨论,解不等式求出a;
点,求出a,b之间的关系,分情况讨论,解不等式求出a;
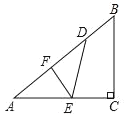
(3)画出函数大致图象和B点和B点关于对称轴对称的点![]() ,根据图可知当A点介于-1和5之间时,
,根据图可知当A点介于-1和5之间时,![]() ,据此可求得
,据此可求得![]() 的取值范围.
的取值范围.
解:(1)二次函数图象的对称轴是![]() .
.
(2)该二次函数的图象经过点![]() ,
,
∴![]() ,∴
,∴![]() ,
,
把![]() 代入
代入![]() ,
,
得![]() .
.
当![]() 时,
时,![]() ,则
,则![]() .
.
而![]() 为整数,∴
为整数,∴![]() ,则
,则![]() ,
,
∴二次函数的表达式为![]() ;
;
当![]() 时,
时,![]() ,则
,则![]() .
.
而![]() 为整数,∴
为整数,∴![]() 或
或![]() ,
,
则对应的![]() 或
或![]() ,
,
∴二次函数的表达式为![]() 或
或![]() .
.
(3)如下图,当a>0时,函数开口向下,对称轴为![]() ,
,
过对称轴取![]() 点的对称点
点的对称点![]() ,
,
∵![]() ,
,
∴![]() ,
,
要使![]() ,
,
则![]() ,即
,即
![]() 解得
解得![]() .
.
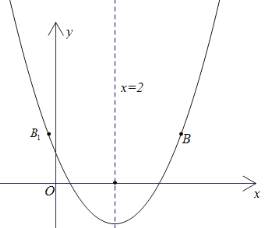
如下图,当a<0时,不存在![]() 时,均有
时,均有![]() 的情况.
的情况.
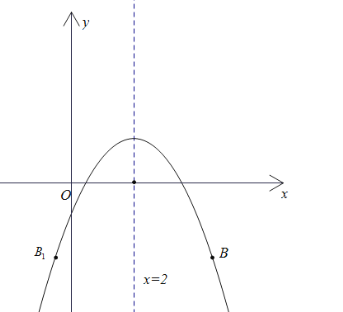

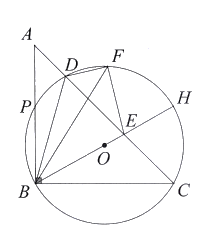
【题目】如图,C是![]() 的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转
的一定点,D是弦AB上的一定点,P是弦CB上的一动点.连接DP,将线段PD绕点P顺时针旋转![]() 得到线段
得到线段![]() .射线
.射线![]() 与
与![]() 交于点Q.已知
交于点Q.已知![]() ,设P,C两点间的距离为xcm,P,D两点间的距离
,设P,C两点间的距离为xcm,P,D两点间的距离![]() ,P,Q两点的距离为
,P,Q两点的距离为![]() .
.
小石根据学习函数的经验,分别对函数![]() ,
,![]() ,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
,随自变量x的变化而变化的规律进行了探究,下面是小石的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() ,与x的几组对应值:
,与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.29 | 3.33 | 1.65 | 1.22 | 1.0 | 2.24 | |
| 0.88 | 2.84 | 3.57 | 4.04 | 4.17 | 3.20 | 0.98 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数据所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() ,
,![]() 的图象;
的图象;
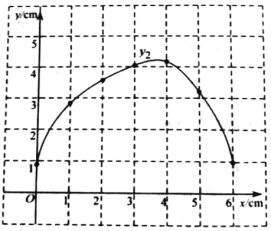
(3)结合函数图象,解决问题:连接DQ,当△DPQ为等腰三角形时,PC的长度约为_____cm.(结果保留一位小数)
【题目】4月23日为世界阅读日,为响应党中央“倡导全民阅读,建设书香会”的号召,某校团委组织了一次全校学生参加的“读书活动”大赛为了解本次赛的成绩,校团委随机抽取了部分学生的成绩(成绩![]() 取整数,总分100分)作为本进行统计,制成如下不完整的统计图表(频数频率分布表和频数分布直方图):
取整数,总分100分)作为本进行统计,制成如下不完整的统计图表(频数频率分布表和频数分布直方图):
成绩 | 频数(人) | 频率 |
| 10 | 0.05 |
| 30 | 0.15 |
| 40 |
|
|
| 0.35 |
| 50 | 0.25 |
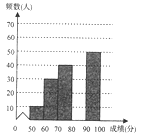
根据所给信息,解答下列问题:
(1)抽取的样本容量是 ;![]() ,
,![]() ;
;
(2)补全频数分布直方图;这200名学生成绩的中位数会落在 分数段;
(3)全校有1200名学生参加比赛,若得分为90分及以上为优秀,请你估计全校参加比赛成绩优秀的学生人数.
【题目】某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
(1)频数分布表中a=____,b=_____,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计跳绳能够一分钟完成160或160次以上的学生有多少人?
(3)已知第一组中有两个甲班学生,第四组中只有一个甲班学生,老师随机从这两个组中各选一名学生谈测试体会,则所选两人正好都是甲班学生的概率是多少?