题目内容
抛物线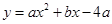 经过
经过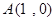 、
、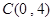 两点,与
两点,与 轴交于另一点
轴交于另一点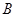 .
.

(1)求抛物线的解析式;
(2)已知点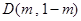 在第二象限的抛物线上,求点
在第二象限的抛物线上,求点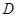 关于直线
关于直线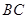 的对称点的坐标;
的对称点的坐标;
(3)在(2)的条件下,连接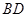 ,点
,点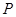 为y轴
为y轴
上一点,且 ,求出点
,求出点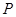 的坐标.
的坐标.
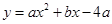 经过
经过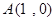 、
、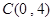 两点,与
两点,与 轴交于另一点
轴交于另一点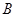 .
.
(1)求抛物线的解析式;
(2)已知点
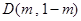 在第二象限的抛物线上,求点
在第二象限的抛物线上,求点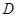 关于直线
关于直线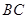 的对称点的坐标;
的对称点的坐标;(3)在(2)的条件下,连接
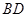 ,点
,点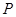 为y轴
为y轴上一点,且
 ,求出点
,求出点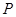 的坐标.
的坐标.(1) y=-x2-3x+4(2)(0,1)(3) (0, )
)
 )
)(1) 因为抛物线
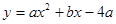 ,经过A(1,0)C(0,4)
,经过A(1,0)C(0,4)把各点代入抛物线得出
a+b-4a=0
-4a=4
解得:a=1,b=-3
故解析式是:
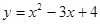
(2) 因为点D(m,m+1)在该抛物线上,故
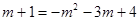
故m=3,
故D(3,4)
因为抛物线与x轴交与另一点B
故B(4,0)
所以直线BC的方程是:y=-x+4
故点D关于直线的对称点的坐标是(1,0)
(3) 由上解知,直线BD的方程是
y=-4x+16
由图分析得出,直线BD的倾斜角是
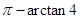
故BP直线的方程为:
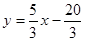
故P(0,
 )
)点评:此类试题属于难度较小的试题,需要考生对此类试题熟练把握,进而学会分析各类函数的解析式的解法

练习册系列答案
相关题目
 与x轴交A,B两点(A点在B点左侧),直线
与x轴交A,B两点(A点在B点左侧),直线 与抛物线交于A,C两点,其中C点的横坐标为2.
与抛物线交于A,C两点,其中C点的横坐标为2.
 轴的平行线交抛物线于E点,求线段PE长度的最大值;
轴的平行线交抛物线于E点,求线段PE长度的最大值;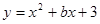 的图象经过点(3,0).
的图象经过点(3,0).
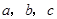 ,用
,用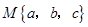 表示这三个数的平均数,用
表示这三个数的平均数,用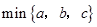 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: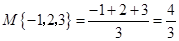 ;
;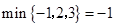 ;
;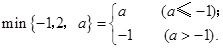
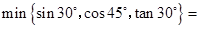 ;
;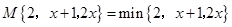 ,求
,求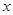 ;
; ,那么 (填
,那么 (填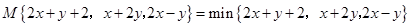 ,则
,则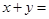 .
.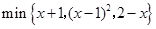 的最大值为 .
的最大值为 .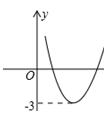
 的对称轴为
的对称轴为 ,则
,则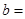 .
.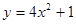

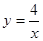
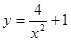
 的图象可能是( )
的图象可能是( )