题目内容
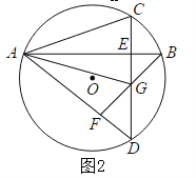
【题目】在平行四边形ABCD中,连接AC,∠CAD=40°,△ABC为钝角等腰三角形,则∠ADC的度数为_____度.
【答案】100或40
【解析】
根据平行四边形的性质得到∠BCA=∠CAD=40°,再由△ABC为钝角等腰三角形,分两种情况分别求出答案即可.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BCA=∠CAD=40°,
∵△ABC为钝角等腰三角形,
∴AB=BC或AB=AC,
①如图1,当AB=BC时,即∠BAC=∠BCA=40°,
∠B=180°﹣40°×2=100°,
则∠ADC=∠B=100°;
②如图2,当AB=AC时,即∠B=∠BCA=40°,
则∠ADC=∠B=40°.
综上所述,∠ADC的度数为100或40度.
故答案为:100或40.

练习册系列答案
相关题目