题目内容
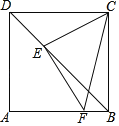
【题目】 AB,CD是![]() 的两条弦,直线AB,CD互相垂直,垂足为点E,连接AD,过点B作
的两条弦,直线AB,CD互相垂直,垂足为点E,连接AD,过点B作![]() ,垂足为点F,直线BF交直线CD于点G.
,垂足为点F,直线BF交直线CD于点G.
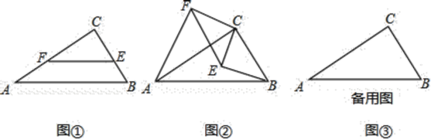
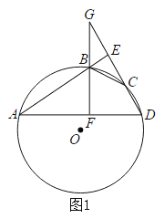
(1)如图1当点E在![]() 外时,连接
外时,连接![]() ,求证BE平分∠GBC;
,求证BE平分∠GBC;
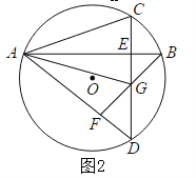
(2)如图2当点E在![]() 内时,连接AC,AG,求证:AC=AG
内时,连接AC,AG,求证:AC=AG
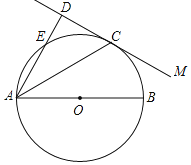
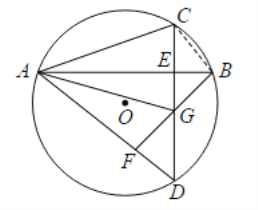
(3)在(2)条件下,连接BO,若BO平分![]() ,求线段EC的长.
,求线段EC的长.
【答案】(1)见解析;(2)见解析;(3)EC=2
【解析】
(1)通过圆内接四边形的性质以及直角三角形中角度的换算证明![]() 即可.
即可.
(2)通过角度换算利用角边角定理证明![]() ,得出
,得出![]() ,最后通过线段垂直平分线性质证得
,最后通过线段垂直平分线性质证得![]() .
.
(3)通过证明![]() 进而得到
进而得到![]() 为等边三角形即可
为等边三角形即可
(1)∵四边形![]() 内接于
内接于![]() .
.
∴![]() ,
,
又∵![]() .
.
∴可得![]() .
.
又∵![]()
∴在![]() 中
中![]() ,
,
同理可得在![]() 中,
中,![]() .
.
∴![]()
∴![]() .
.
又∵![]() .
.
∴![]()
即![]() 平分
平分![]()
(2)如图所示,连接![]() ,
,
∵![]()
∴在![]() 中
中![]()
同理可得![]() ,
,
∴![]() ,
,
由同弧所对的圆周角相等可得
![]() .
.
又∵![]()
∴![]() .
.
在![]() 和
和![]() 中,
中,
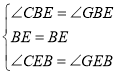
∴![]()
∴![]() .
.
∴AB垂直平分CG
∴![]()
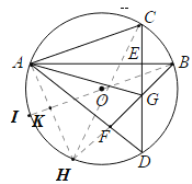
(3)延长![]() 交
交![]() 于H,连接
于H,连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于K交
于K交![]() 于I.
于I.
∵![]()
∴![]()
∵![]()
![]() ,即
,即![]()
∵![]() 平分
平分![]() 且过圆心
且过圆心![]() ,
,
∴![]() 垂直平分
垂直平分![]()
∴![]()
∴![]()
∴![]()
又∵![]() .
.
∴![]()
∴![]()
∵![]() ,
,
∴![]() 为等边三角形
为等边三角形
∴![]()
又∵![]()
∴![]()

练习册系列答案
相关题目