题目内容
【题目】图(1)所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图(2)所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )
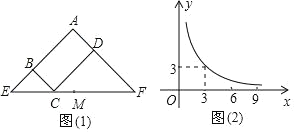
A.当x=3时,EC<EM
B.当y=9时,EC>EM
C.当x增大时,ECCF的值增大
D.当x变化时,四边形BCDA的面积不变
【答案】D
【解析】
利用矩形的性质及等腰直角三角形的性质可得出AB=CD,∠E=∠F=45°,进而可得出△BEC和△CDF均为等腰直角三角形,结合BC=x,CD=y可得出EC=![]() x,CF=
x,CF=![]() y,EF=
y,EF=![]() (x+y),再利用反比例函数图象上点的坐标特征可得出xy=9.
(x+y),再利用反比例函数图象上点的坐标特征可得出xy=9.
A、代入x=3可求出y,EC,EF的长,再结合M为EF的中点可得出EM=3![]() =EC,选项A不符合题意;
=EC,选项A不符合题意;
B、代入y=9可求出x,EC,EM的长,进而可得出EC<EM,选项B不符合题意;
C、由EC=![]() x,CF=
x,CF=![]() y可得出ECCF=2xy=2×9=18,选项C不符合题意;
y可得出ECCF=2xy=2×9=18,选项C不符合题意;
D、利用矩形的面积公式结合xy=9可得出S矩形BCDA=xy=9,进而可得出当x变化时,四边形BCDA的面积不变,选项D符合题意.
此题得解.
解:∵四边形ABCD为矩形,
∴AB=CD.
∵△AEF为等腰直角三角形,
∴∠E=∠F=45°,
∴△BEC和△CDF均为等腰直角三角形.
∵BC=x,CD=y,
∴AE=x+y,
∴EC=![]() x,CF=
x,CF=![]() y,EF=
y,EF=![]() (x+y).
(x+y).
∵y与x满足的反比例函数关系,且点(3,3)在该函数图象上,
∴xy=9.
A、当x=3时,y=![]() =3,EC=3
=3,EC=3![]() ,EF=6
,EF=6![]() .
.
又∵M为EF的中点,
∴EM=3![]() =EC,选项A不符合题意;
=EC,选项A不符合题意;
B、当y=9时,x=1,
∴EC=![]() ,EM=
,EM=![]() EF=5
EF=5![]() ,
,
∴EC<EM,选项B不符合题意;
C、∵EC=![]() x,CF=
x,CF=![]() y,
y,
∴ECCF=2xy=2×9=18,选项C不符合题意;
D、∵S
∴当x变化时,四边形BCDA的面积不变,选项D符合题意.
故选:D.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案