��Ŀ����
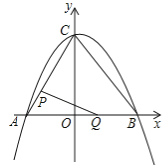
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У����κ���y��![]() x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��
x2+bx+c��ͼ���������ύ��A��B��C���㣬���е�A������Ϊ����3��0������B������Ϊ��4��0��������AC��BC������P�ӵ�A���������߶�AC����ÿ��1����λ���ȵ��ٶ����C�������˶���ͬʱ������Q�ӵ�O���������߶�OB����ÿ��1����λ���ȵ��ٶ����B�������˶���������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶������˶�ʱ��Ϊt�룮����PQ��
��1����գ�b�� ��c�� ��
��2���ڵ�P��Q�˶������У���APQ������ֱ������������˵�����ɣ�
��3����M���������ϣ��ҡ�AOM��������AOC�������ȣ������M�����ꡣ
���𰸡���1��![]() ��4����2����������ֱ�������Σ�����������3��M(1,4)��M(
��4����2����������ֱ�������Σ�����������3��M(1,4)��M(![]() ,-4����M(
,-4����M(![]() ,-4��
,-4��
��������
(1)�������ߵĽ���ʽΪy=a��x+3����x-4������a=-![]() ����ɵõ������ߵĽ���ʽ���Ӷ���ȷ����b��c��ֵ��
����ɵõ������ߵĽ���ʽ���Ӷ���ȷ����b��c��ֵ��
��2������õ�C�����꣬���ݹ��ɶ��������AC=5����PC=5-t��AQ=3+t,���жϵ���APQ��ֱ��������ʱ�����APQ��90�����Ӷ��ó�![]() AOC
AOC![]() APQ���õ�����ʽ�з�����⼴�ɣ�
APQ���õ�����ʽ�з�����⼴�ɣ�
(3)���ݵ�M���������ϣ������M������Ϊ��m����![]() m2+
m2+![]() m+4�����ٸ�����AOM���������AOC�������ȣ��Ӷ��ó���
m+4�����ٸ�����AOM���������AOC�������ȣ��Ӷ��ó���![]() m2+
m2+![]() m+4=
m+4=![]() ���ⷽ�̼��ɣ�
���ⷽ�̼��ɣ�
�⣺��1���������ߵĽ���ʽΪy��a��x+3����x��4������a����![]() ����ã�y����
����ã�y����![]() x2+
x2+![]() x+4��
x+4��
��b��![]() ��c��4��
��c��4��
��2���ڵ�P��Q�˶������У���APQ��������ֱ�������Σ�
�������£����ڵ�P��Q�˶������У���PAQ����PQAʼ��Ϊ��ǣ�
�൱��APQ��ֱ��������ʱ�����APQ��90����
��x��0���������ߵĽ���ʽ�ã�y��4��
��C��0��4�����ߵ�A������Ϊ����3��0����
����Rt��AOC�У����ݹ��ɶ����ã�AC��5��
��AP��OQ��t����AQ=3+t��
�ߡ�OAC����PAQ����APQ����AOC
��![]() AOC
AOC![]() APQ
APQ
��AP:AO=AQ:AC
��![]() =
=![]() ��t=4.5��
��t=4.5��
���������֪��0��t��4��
��t��4.5�������⣬����APQ��������ֱ�������Σ�
(3 )���M��������m����![]() m2+
m2+![]() m+4��
m+4��
�ߡ�AOM���������AOC�������ȣ��ҵ�ΪAO��C��0��4����
�ੁ![]() m2+
m2+![]() m+4=
m+4=![]()
����![]() m2+
m2+![]() m+4=-4ʱ����ã�m=
m+4=-4ʱ����ã�m=![]() ��
��![]() ,
,
����![]() m2+
m2+![]() m+4=4ʱ����ã�m=1��0
m+4=4ʱ����ã�m=1��0
�ߵ�m=0ʱ����C�غϣ���m=![]() ��
��![]() ��1
��1
�� M(1,4)��M(![]() ,-4����M(
,-4����M(![]() ,-4��
,-4��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�