题目内容
【题目】现有一段120m的篱笆,准备用这些篱笆借助一段墙角围成如图所示两块面积相同的矩形场地养鸡.
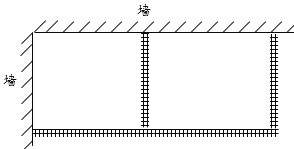
(1)如图所示,若围成的场地总面积为1750m2,则该场地的宽(图中纵向)应为多少?
(2)能不能围成面积为2000m2的场地?若能,求出此时篱笆的宽;若不能,求围成场地面积的最大值.
【答案】(1)![]() ;(2)1800 m2
;(2)1800 m2
【解析】
(1)设该场地的宽(图中纵向)为x(m),场地的面积y(m2),列出y与x的函数关系式,将1750代入式中,得到方程,解方程可得;
(2)将y=2000代入函数关系式中,可得方程,根据方程的根的判别式,可得结论,再由二次函数的顶点式可得出面积的最大值.
解:设该场地的宽(图中纵向)为x(m),场地的面积y(m2), 得:
![]()
(1)若围成场地的面积为1750 m2,根据题意可得:
![]()
解这个方程得:![]()
∴当宽为25m或35m时,能围成面积为1750 m2的场地.
(2)若围成场地的面积为2000 m2,根据题意可得
![]()
整理得![]()
∵Δ=![]() <0
<0
所以所得方程无实数根,不能围成面积为2000 m2的场地
∵![]()
∴当![]() 时,场地的面积取得最大值1800.
时,场地的面积取得最大值1800.
所以围成场地面积的最大值为1800 m2

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目