题目内容
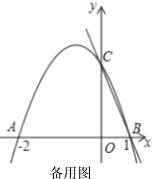
【题目】如图,在平面直角坐标系中,直线y=kx﹣![]() 与抛物线y=ax2+bx+
与抛物线y=ax2+bx+![]() 交于点A、C,与y轴交于点B,点A的坐标为(2,0),点C的横坐标为﹣8.
交于点A、C,与y轴交于点B,点A的坐标为(2,0),点C的横坐标为﹣8.
(1)请直接写出直线和抛物线的解析式;
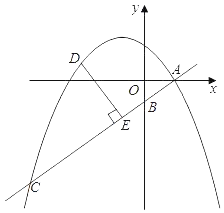
(2)点D是直线AB上方的抛物线上一动点(不与点A、C重合),作DE⊥AC于点E.设点D的横坐标为m.求DE的长关于m的函数解析式,并写出DE长的最大值;
(3)平移△AOB,使平移后的三角形的三个顶点中有两个在抛物线上,请直接写出平移后的点A对应点A′的坐标.
【答案】(1)![]() ;(2)DE的最大值为5;(3)点A′(﹣
;(2)DE的最大值为5;(3)点A′(﹣![]() ,
,![]() )或(﹣2,3)
)或(﹣2,3)
【解析】
(1)将点A,C坐标代入一次函数与二次函数表达式,即可解题,
(2)根据DE= DFsin∠DFE=![]() ·(﹣
·(﹣![]() m2﹣
m2﹣![]() m+4)=﹣
m+4)=﹣![]() (m+3)2+5即可求解,
(m+3)2+5即可求解,
(3)分别设出平移后的点A,B,O的坐标,根据有两个点在二次函数图形上,代入解方程组即可解题.
(1)将点A坐标代入直线表达式得:0=2k﹣![]() ,解得:k=
,解得:k=![]() ,
,
故一次函数表达式为:y=![]() x﹣
x﹣![]() ,则点C坐标为(﹣8,﹣
,则点C坐标为(﹣8,﹣![]() ),
),
同理,将点A、C的坐标代入二次函数表达式并解得二次函数表达式为:![]() ;
;
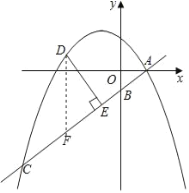
(2)作DF∥y轴交直线AB于点F,
∴∠DFE=∠OBA,(同角的余角相等)
设点D的横坐标为m,则点D(m,﹣![]() m2﹣
m2﹣![]() m+
m+![]() ),点F(m,
),点F(m,![]() m﹣
m﹣![]() ),
),
DF=﹣![]() m2﹣
m2﹣![]() m+
m+![]() ﹣(
﹣(![]() m﹣
m﹣![]() )=﹣
)=﹣![]() m2﹣
m2﹣![]() m+4,
m+4,
AB=![]() =
=![]() ,sin∠DFE=sin∠OBA=
,sin∠DFE=sin∠OBA=![]() ,
,
∴DE=DFsin∠DFE=![]() ·(﹣
·(﹣![]() m2﹣
m2﹣![]() m+4)=﹣
m+4)=﹣![]() (m+3)2+5,
(m+3)2+5,
故:DE的最大值为5;
(3)设三角形向左平移m个、向上平移n个单位时,三角形有2个顶点在抛物线上,
①当平移后点A和O在抛物线上时,
则平移后点A、O的坐标分别为(2﹣m,n)、(﹣m,n),
将上述两个点坐标代入二次函数表达式得:
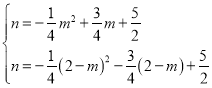
解得:m=![]() ,n=
,n=![]() ,
,
②当平移后点A和B在抛物线上时,平移后点A、B的坐标分别为(2﹣m,n)、(﹣m,n-![]() ),
),
同理可得:点A′(﹣2,3),
即点A′(﹣![]() ,
,![]() )或(﹣2,3).
)或(﹣2,3).