Question

【题目】如图，大楼AD与塔CB之间的距离AC长为27m，某人在楼底A处测得塔顶的仰角为60°，爬到楼顶D处测得塔顶B的仰角为30°，分别求大楼AD的高与塔BC的高（结果精确到0.1m，参考数据：≈2.24，≈1.732，≈1.414）

Answer 1

【答案】大楼AD的高约31.2m，塔BC的高约46.8m．

【解析】

先解Rt△DBE,求出BE=9,再解Rt△ABC,求出BC=27≈46.8,那么

AD=CE=27-9=18≈31.2.

解：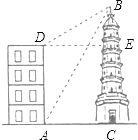

由题意，可知∠BDE=30°，∠BAC=60°，四边形ACED是矩形，

∴DE=AC=27．

在Rt△DBE中，

tan∠BDE= ，

∴=，

∴BE=9．

在Rt△ABC中，

tan∠BAC= ，

∴=，

∴BC=27≈46.8，

AD=CE=27﹣9=18≈31.2．

答：大楼AD的高约31.2m，塔BC的高约46.8m．