题目内容
如图,已知二次函数y=-x2+bx+c的图象与x轴交于点A、B,与y轴交于点C,其顶点为D,且直线DC的解析式为y=x+3.
(1)求二次函数的解析式;
(2)求△ABC外接圆的半径及外心的坐标;
(3)若点P是第一象限内抛物线上一动点,求四边形ACPB的面积最大值.

(1)求二次函数的解析式;
(2)求△ABC外接圆的半径及外心的坐标;
(3)若点P是第一象限内抛物线上一动点,求四边形ACPB的面积最大值.

(1)∵二次函数:y=-x2+bx+c的图象与直线DC:y=x+3交于点C,
∴c=3,C(0,3);
二次函数 y=-x2+bx+3中,顶点D (
,
),代入直线DC y=x+3中,得:
+3=
,
解得 b1=0(舍)、b2=2;
故二次函数的解析式:y=-x2+2x+3.
(2)由(1)的抛物线解析式知:A(-1,0)、B(3,0)、C(0,3);
设△ABC的外心M(x,y),则:
AM2=(x+1)2+y2、BM2=(x-3)2+y2、CM2=x2+(y-3)2;
由于AM=BM=CM,所以有:
,
解得
此时 AM=BM=CM=
;
综上,△ABC的外接圆半径为
,外心的坐标(1,1).
 (3)如右图,过点P作PE∥y轴,交直线BC于点E;
(3)如右图,过点P作PE∥y轴,交直线BC于点E;
由B(3,0)、C(0,3)知,直线BC:y=-x+3;
设点P(x,-x2+2x+3),则E(x,-x+3),
PE=-x2+2x+3-(-x+3)=-x2+3x;
则S四边形ACPB=S△ACB+S△CPB
=
AB•OC+
PE•OB
=
×4×3+
×(-x2+3x)×3
=-
(x-
)2+
;
综上,四边形ACPB的最大面积最大值为
.
∴c=3,C(0,3);
二次函数 y=-x2+bx+3中,顶点D (
| b |
| 2 |
| b2+12 |
| 4 |
| b |
| 2 |
| b2+12 |
| 4 |
解得 b1=0(舍)、b2=2;
故二次函数的解析式:y=-x2+2x+3.
(2)由(1)的抛物线解析式知:A(-1,0)、B(3,0)、C(0,3);
设△ABC的外心M(x,y),则:
AM2=(x+1)2+y2、BM2=(x-3)2+y2、CM2=x2+(y-3)2;
由于AM=BM=CM,所以有:
|
解得
|
此时 AM=BM=CM=
| 5 |
综上,△ABC的外接圆半径为
| 5 |
 (3)如右图,过点P作PE∥y轴,交直线BC于点E;
(3)如右图,过点P作PE∥y轴,交直线BC于点E;由B(3,0)、C(0,3)知,直线BC:y=-x+3;
设点P(x,-x2+2x+3),则E(x,-x+3),
PE=-x2+2x+3-(-x+3)=-x2+3x;
则S四边形ACPB=S△ACB+S△CPB
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
| 3 |
| 2 |
| 75 |
| 8 |
综上,四边形ACPB的最大面积最大值为
| 75 |
| 8 |

练习册系列答案
相关题目
 60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.
60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.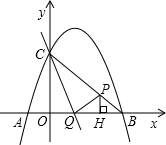 0,3)的直线y=-
0,3)的直线y=-
 位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF.
位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度EF.
