��Ŀ����
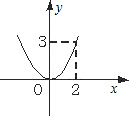
��ͼ����֪������y=-
x2+bx+c�������ύ��A��B��C���㣬��A�ĺ�����Ϊ-1������C��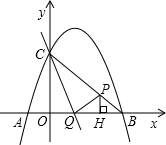 0��3����ֱ��y=-
0��3����ֱ��y=-
x+3��x�ύ�ڵ�Q����P���߶�BC�ϵ�һ�����㣬PH��OB�ڵ�H����PB=5t����0��t��1��
��1��ȷ��b��c��ֵ��
��2��д����B��Q��P�����꣨����Q��P�ú�t��ʽ�ӱ�ʾ����
��3������P�ı仯���Ƿ����t��ֵ��ʹ��PQBΪ���������Σ������ڣ��������t��ֵ���������ڣ�˵�����ɣ�
| 3 |
| 4 |
 0��3����ֱ��y=-
0��3����ֱ��y=-| 3 |
| 4t |
��1��ȷ��b��c��ֵ��
��2��д����B��Q��P�����꣨����Q��P�ú�t��ʽ�ӱ�ʾ����
��3������P�ı仯���Ƿ����t��ֵ��ʹ��PQBΪ���������Σ������ڣ��������t��ֵ���������ڣ�˵�����ɣ�
��1����֪�����߹�A��-1��0����C��0��3�������У�
��
���
��
���b=
��c=3��
��2���������ߵĽ���ʽ��y=0������-
x2+
x+3=0��
���x=-1��x=4��
��B��4��0����OB=4��
���BC=5��
��ֱ��������OBC�У�OB=4��OC=3��BC=5��
��sin��CBO=
��cos��CBO=
��
��ֱ��������BHP�У�BP=5t��
���PH=3t��BH=4t��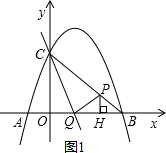
��OH=OB-BH=4-4t��
���P��4-4t��3t����
��ֱ�ߵĽ���ʽ��y=0������0=-
x+3��x=4t��
��Q��4t��0����
��3������t��ֵ���������������
����ͼ1����PQ=PBʱ��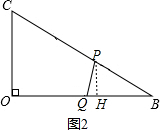
��PH��OB����QH=HB��
��4-4t-4t=4t��
��t=
��
�ڵ�PB=QB��4-4t=5t��
��t=
��
�۵�PQ=QBʱ����Rt��PHQ����QH2+PH2=PQ2��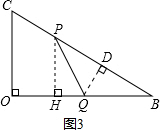
�ࣨ8t-4��2+��3t��2=��4-4t��2��
��57t2-32t=0��
��t=
��t=0����ȥ����
�֡�0��t��1��
�൱t=
��
��
ʱ����PQBΪ���������Σ�
|
���
|
���b=
| 9 |
| 4 |
��2���������ߵĽ���ʽ��y=0������-
| 3 |
| 4 |
| 9 |
| 4 |
���x=-1��x=4��
��B��4��0����OB=4��
���BC=5��
��ֱ��������OBC�У�OB=4��OC=3��BC=5��
��sin��CBO=
| 3 |
| 5 |
| 4 |
| 5 |
��ֱ��������BHP�У�BP=5t��
���PH=3t��BH=4t��

��OH=OB-BH=4-4t��
���P��4-4t��3t����
��ֱ�ߵĽ���ʽ��y=0������0=-
| 3 |
| 4t |
��Q��4t��0����
��3������t��ֵ���������������
����ͼ1����PQ=PBʱ��

��PH��OB����QH=HB��
��4-4t-4t=4t��
��t=
| 1 |
| 3 |
�ڵ�PB=QB��4-4t=5t��
��t=
| 4 |
| 9 |
�۵�PQ=QBʱ����Rt��PHQ����QH2+PH2=PQ2��

�ࣨ8t-4��2+��3t��2=��4-4t��2��
��57t2-32t=0��
��t=
| 32 |
| 57 |
�֡�0��t��1��
�൱t=
| 1 |
| 3 |
| 4 |
| 9 |
| 32 |
| 57 |

��ϰ��ϵ�д�
 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
�����Ŀ
 ����B������Ϊ��3��0������ֱ��y=kx��y������ƽ��3����λ���Ⱥ�ǡ�þ���B��C���㣮
����B������Ϊ��3��0������ֱ��y=kx��y������ƽ��3����λ���Ⱥ�ǡ�þ���B��C���㣮