题目内容
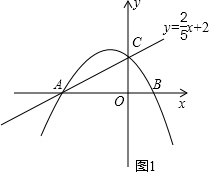
已知抛物线y=ax2+bx+c与y轴的交点为C,顶点为M,直线CM的解析式y=-x+2并且线段CM的长为2
,
(1)求抛物线的解析式.
(2)设抛物线与x轴有两个交点A(x1,0)、B(x2,0),且点A在B的左侧,求线段AB的长.
| 2 |
(1)求抛物线的解析式.
(2)设抛物线与x轴有两个交点A(x1,0)、B(x2,0),且点A在B的左侧,求线段AB的长.
(1)令x=0,则y=2,
所以,点C(0,2),
∵点M在直线y=-x+2上,
∴设点M的坐标为M(x,-x+2),
由勾股定理得CM=
=2
,
整理得,x2=4,
解得x1=2,x2=-2,
当x1=2时,y1=-2+2=0,
当x2=-2,y2=-(-2)+2=4
∴M(-2,4)或M(2,0),
当M(-2,4)时,设抛物线解析式为y=a(x+2)2+4,
∵抛物线过点C(0,2),
∴a(0+2)2+4=2,
解得a=-
,
∴y=-
x2-2x+2,
当M(2,0)时,设抛物线解析式为y=a(x-2)2,
∵抛物线过点C(0,2)点,
∴a(0-2)2=2,
解得a=
,
∴y=
x2-2x+2,
∴所求抛物线为:y=-
x2-2x+2或y=
x2-2x+2;
(2)∵抛物线与x轴有两个交点,
∴y=
x2-2x+2不合题意,舍去.
∴抛物线应为:y=-
x2-2x+2,
令y=0,则-
x2-2x+2=0,
整理得,x2+4x-4=0,
解得x1=-2+2
,x2=-2-2
,
∵点A在B的左侧,
∴点A(-2-2
,0),B(-2+2
,0),
∴AB=(-2+2
)-(-2-2
)=4
.
所以,点C(0,2),
∵点M在直线y=-x+2上,
∴设点M的坐标为M(x,-x+2),
由勾股定理得CM=
| x2+(-x+2-2)2 |
| 2 |
整理得,x2=4,
解得x1=2,x2=-2,
当x1=2时,y1=-2+2=0,
当x2=-2,y2=-(-2)+2=4
∴M(-2,4)或M(2,0),
当M(-2,4)时,设抛物线解析式为y=a(x+2)2+4,
∵抛物线过点C(0,2),
∴a(0+2)2+4=2,
解得a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
当M(2,0)时,设抛物线解析式为y=a(x-2)2,
∵抛物线过点C(0,2)点,
∴a(0-2)2=2,
解得a=
| 1 |
| 2 |
∴y=
| 1 |
| 2 |
∴所求抛物线为:y=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵抛物线与x轴有两个交点,
∴y=
| 1 |
| 2 |
∴抛物线应为:y=-
| 1 |
| 2 |
令y=0,则-
| 1 |
| 2 |
整理得,x2+4x-4=0,
解得x1=-2+2
| 2 |
| 2 |
∵点A在B的左侧,
∴点A(-2-2
| 2 |
| 2 |
∴AB=(-2+2
| 2 |
| 2 |
| 2 |

练习册系列答案
相关题目



 ,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
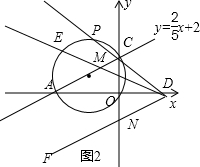


 的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.
的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.