题目内容
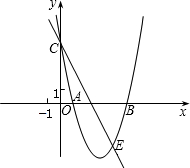
二次函数y1=ax2-2bx+c和y2=(a+1)•x2-2(b+2)x+c+3在同一坐标系中的图象如图所示,若OB=OA,BC=DC,且点B,C的横坐标分别为1,3,求这两个函数的解析式.


∵OB=OA,
∴二次函数y1=ax2-2bx+c的对称轴为y轴,
∴-
=0,
解得b=0,
∵BC=DC,
∴二次函数y=(a+1)•x2-2(b+2)x+c+3的顶点为C,
∵点C的横坐标为3,
∴-
=3,
解得a=-
,
∵点B的横坐标为1,
∴-
×12-2×0×1+c=0,
解得c=
,
所以,y1=-
x2+
,y2=
x2-4x+
.
∴二次函数y1=ax2-2bx+c的对称轴为y轴,
∴-
| 2b |
| 2a |
解得b=0,
∵BC=DC,
∴二次函数y=(a+1)•x2-2(b+2)x+c+3的顶点为C,
∵点C的横坐标为3,
∴-
| -2(b+2) |
| 2(a+1) |
解得a=-
| 1 |
| 3 |
∵点B的横坐标为1,
∴-
| 1 |
| 3 |
解得c=
| 1 |
| 3 |
所以,y1=-
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 10 |
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.
,OB=4,现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD,已知一抛物线经过C、D、B三点.
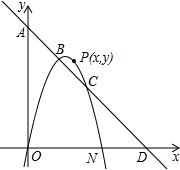


 的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.
的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.