题目内容
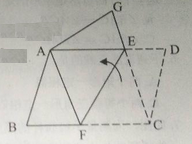
【题目】如图,将一张平行四边形纸片ABCD沿着线段EF折叠(点E、F分别在AB边和BC边上),使得点C落在点A处,点D落在点G出。
(1)如果连接EC,那么线段GE与EC在同一条直线上吗?为什么?
(2)试判断四边形AFCE的形状,并说明你是怎样判断的?
【答案】(1)线段GE与EC在同一条直线上,证明详见解析;(2)四边形AFCE是菱形,证明详见解析.
【解析】
(1)根据题意易证△AGE≌△CDE,根据全等三角形的性质可得∠GEA=∠DEC,再根据∠DEC+∠AEC=180°,即可得∠DEA+∠AEC=180°;
(2)证明出AF=FC=EC=AE即可得四边形AFCE是菱形.
(1)线段GE与EC在同一条直线上
证明:∵在△AGE和△CDE中
AG=CD,∠G=∠D,DE=GE
∴△AGE≌△CDE
∴∠GEA=∠DEC
∵∠DEC+∠AEC=180°
∴∠DEA+∠AEC=180°
∴线段GE与EC在同一条直线上
(2)四边形AFCE是菱形,证明如下:
证明:由题知,∠AFE=∠CFE
∵AE∥BC ∴∠EFC=∠AEF ∴∠AFE=∠AEF ∴AF=AE
由(1)知AE=EC,∵AF=FC ∴AF=FC=EC=AE ∴四边形AFCE是菱形

【题目】为提醒人们节约用水,及时修好漏水的水龙头.小明同学做了水龙头漏水实验,每隔10秒观察量筒中水的体积,记录的数据如表(漏出的水量精确到1毫升),已知用于接水的量筒最大容量为100毫升.
时间t(秒) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
量筒内水量v(毫升) | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
(1)在图中的平面直角坐标系中,以(t,v)为坐标描出上表中数据对应的点;
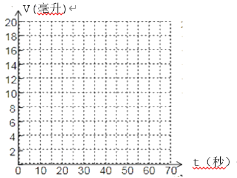
(2)用光滑的曲线连接各点,你猜测V与t的函数关系式是______________.
(3)解决问题:
①小明同学所用量筒开始实验前原有存水 毫升;
②如果小明同学继续实验,当量筒中的水刚好盛满时,所需时间是_____秒;
③按此漏水速度,半小时会漏水 毫升.