题目内容
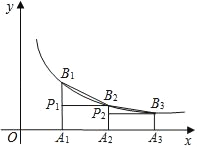
【题目】如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3=…=An﹣1An=1,分别过点A1、A2、A3、An作x轴的垂线,交反比例函数y=![]() (x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.
(x>0)的图象于点B1、B2、B3、…、Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2,…,若记△B1P1B2的面积为S1,△B2P2B3的面积为S2,…,△BnPnBn+1的面积为Sn,则S1+S2+…+S2018=_____.
【答案】![]()
【解析】分析:
由题意易得B1、B2、B3、![]() 、Bn的坐标分别为:(1,2),(2,1),(3,
、Bn的坐标分别为:(1,2),(2,1),(3,![]() )、
)、![]() 、(n,
、(n,![]() ),从而可得B1P1=2﹣1=1,B2P2=1﹣
),从而可得B1P1=2﹣1=1,B2P2=1﹣![]() =
=![]() ,B3P3=
,B3P3=![]() ﹣
﹣![]() =
=![]() ,…,BnPn=
,…,BnPn=![]() ﹣
﹣![]() =
=![]() ,由此可得Sn=
,由此可得Sn=![]() AnAn+1BnPn=
AnAn+1BnPn=![]() ,从而可得S1+S2+…+S2018=
,从而可得S1+S2+…+S2018=![]() ,再展开计算即可.
,再展开计算即可.
详解:
根据题意可知:点B1(1,2)、B2(2,1)、B3(3,![]() )、…、Bn(n,
)、…、Bn(n,![]() ),
),
∴B1P1=2﹣1=1,B2P2=1﹣![]() =
=![]() ,B3P3=
,B3P3=![]() ﹣
﹣![]() =
=![]() ,…,BnPn=
,…,BnPn=![]() ﹣
﹣![]() =
=![]() ,
,
∴Sn=![]() AnAn+1BnPn=
AnAn+1BnPn=![]() ,
,
∴S1+S2+…+S2018
=![]()
=![]()
=![]()
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目