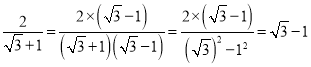题目内容
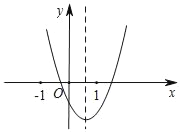
【题目】如图1,已知抛物线![]() 与x轴从左至右交于A,B两点,与y轴交于点c.
与x轴从左至右交于A,B两点,与y轴交于点c.

(1)若抛物线过点T(1,-![]() ),求抛物线的解析式;
),求抛物线的解析式;
(2)在第二象限内的抛物线上是否存在点D,使得以A、B、D三点为顶点的三角形与△ABC相似?若存在,求a的值;若不存在,请说明理由.
(3)如图2,在(1)的条件下,点P的坐标为(-1,1),点Q(6,t)是抛物线上的点,在x轴上,从左至右有M、N两点,且MN=2,问MN在x轴上移动到何处时,四边形PQNM的周长最小?请直接写出符合条件的点M的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)M(-
;(3)M(-![]() ,0)
,0)
【解析】
(1)把T的坐标代入解析式,求出a的值,写出解析式;
(2)根据点D在第二象限,∠DAB为钝角,所以当A、B、D三点为顶点的三角形与△ABC相似时,只能∠DAB与∠ACB对应,所以分以下两种情况讨论:①如图2,当△BDA∽△ABC时,∠BAC=∠ABD,
②当△DBA∽△ABC时,如图3,∠ABC=∠ABD,分别列比例式,得方程求解;
(3)本题介绍两种解法:
解法一:先求出Q的坐标为(6,10),通过轴对称作出使四边形PQNM的周长最小时的M、N的位置,因为PQ、NM为定值,要想周长最小,则需要PM+NQ最小,即想办法做到一直线上,因此作P关于x轴的对称点P′,找到P′G=2,且P′G∥x轴,利用平移构建平行四边形P′GNM,从而得到x轴上的M和N,求出M的坐标.
解法二:同理得Q的坐标,作P关于x轴的对称点P′,过Q作QH∥x轴,交y轴于H,在QH上从Q起取一点Q',使QQ'=2,连接Q'P',交x轴于一点,则此点为M,根据P'Q'的解析式可得M的坐标.
(1)如图1,把T(1,﹣![]() )代入抛物线y=
)代入抛物线y=![]() (x﹣2)(x+a)得:
(x﹣2)(x+a)得:
﹣![]() =
=![]() (1﹣2)(1+a),
(1﹣2)(1+a),
解得:a=4,
∴抛物线的解析式为:y=![]() x2+
x2+![]() x﹣2;
x﹣2;
(2)当x=0时,y=![]() ×(﹣2)×a=﹣2,
×(﹣2)×a=﹣2,
∴C(0,﹣2),
当y=0时,![]() (x﹣2)(x+a)=0,
(x﹣2)(x+a)=0,
x1=2,x2=﹣a,
∴A(﹣a,0)、B(2,0),
如图2,过D作DE⊥x轴于E,
设D(m,n),
∵点D在第二象限,∠DAB为钝角,
∴分两种情况:
①如图2,当△BDA∽△ABC时,∠BAC=∠ABD,
∴tan∠BAC=tan∠ABD,即![]() ,
,
∴![]() ,
,
n=![]() ,
,
则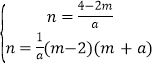 ,
,
解得:m=﹣2﹣a或2,
∴E(﹣2﹣a,0),
由勾股定理得:AC=![]() ,
,
∵![]() ,
,
∴![]() ,
,
BD=![]() ,
,
∵△BDA∽△ABC,
∴![]() ,
,
∴AB2=ACBD,
即(a+2)2=![]() ,
,
解得:0=16,此方程无解;
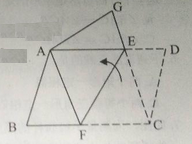
②当△DBA∽△ABC时,如图3,∠ABC=∠ABD,
∵B(2,0),C(0,﹣2),
∴OB=OC=2,
∴△OBC是等腰直角三角形,
有BC=2![]() ,
,
∴∠OCB=∠OBC=45°,
∴∠ABC=∠ABD=45°,
∴DE=BE,
n=﹣m+2,
∴BD=![]() ,
,
∵△DBA∽△ABC,
∴![]() ,
,
∴AB2=BDBC,
∴(a+2)2=![]() 2
2![]() =4n,
=4n,
则 ,
,
解得: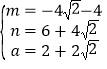 ,
,
则a=2+2![]() ;
;
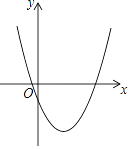
(3)解法一:当x=6时,y=![]() (6﹣2)(6+4)=10,
(6﹣2)(6+4)=10,
∴Q(6,10),
如图4,作P关于x轴的对称点P′,过P′作P′G∥x轴,且P′G=2,连接GQ交x轴于N,过P′作P′M∥GN,交x轴于M,
此时,QG就是MP+NQ的最小值,由于PQ、NM为定值,所以此时,四边形PMNQ的周长最小,
∵P(﹣1,1),
∴P′(﹣1,﹣1),
∵P′G∥MN,P′M∥GN,
∴四边形P′GNM是平行四边形,
∴MN=P′G=2,NG=P′M=PM,
∴G(1,﹣1),
设GQ的解析式为:y=kx+b,
把G(1,﹣1)和Q(6,10)代入得:![]() ,
,
解得: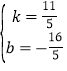 ,
,
∴GQ的解析式为:y= 当y=0时,x= ∴N( ∵MN=2, ∴M(﹣ 解法二:如图5,同理得Q(6,10), P(﹣1,1)关于x轴的对称点P′(﹣1,﹣1),过Q作QH∥x轴,交y轴于H,在QH上从Q起取一点Q',使QQ'=2,连接Q'P',交x轴于一点,则此点为M,此时,四边形PMNQ的周长最小, ∵Q'(4,10),P′(﹣1,﹣1), 易得P'Q'的解析式为:y= 当y=0时, ∴M(﹣![]() x﹣
x﹣![]() ,
,![]() ,
,![]() ,0),
,0),![]() ,0).
,0).![]() x+
x+![]() ,
,![]() x+
x+![]() =0,x=﹣
=0,x=﹣![]() ,
,![]() ,0).
,0).

 阅读快车系列答案
阅读快车系列答案