题目内容
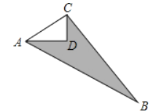
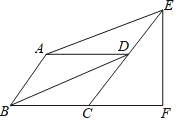
【题目】如图,平行四边形ABCD中,E,F分别在CD、BC的延长线上,AE∥BD,EF⊥BC,tan∠ABC=![]() ,EF=,则AB的长为( )
,EF=,则AB的长为( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
【答案】B
【解析】
由平行四边形性质得出AB=CD,AB∥CD,证出四边形ABDE是平行四边形,得出DE=DC=AB,再由平行线得出∠ECF=∠ABC,由三角函数求出CF长,再用勾股定理CE,即可得出AB的长.
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴AB=DE=CD,即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠ECF=∠ABC,
∴tan∠ECF=tan∠ABC=![]() ,
,
在Rt△CFE中,EF=![]() ,tan∠ECF=
,tan∠ECF=![]() =
=![]() =
=![]() ,
,
∴CF=![]() ,
,
根据勾股定理得,CE=![]() =
=![]() ,
,
∴AB=![]() CE=
CE=![]() ,
,
故选:B.

练习册系列答案
相关题目