Question

【题目】如图，在平面直角坐标系中，直线与轴交于点，与轴交于点 ，与直线相交于点 ，

（1）求直线 的函数表达式；

（2）求 的面积；

（3）在 轴上是否存在一点 ，使是等腰三角形．若不存在，请说明理由；若存在，请直接写出点 的坐标

Answer 1

【答案】（1）；（2）12；（3）存在，

【解析】

（1）将点A、B的坐标代入解析式，即可得到答案；

（2）先求出交点C的坐标，利用底乘高列式计算即可得到答案；

（3）先求出OC的长，分三种情况求出点P的坐标使是等腰三角形.

（1）由题意得，解得，直线的函数表达式；

（2）解方程组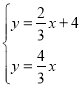，得，

∴点的坐标，

∴ ；

（3）存在，

,

当OP=OC时，点P(10，0),(-10，0),

当OC=PC时，点P（12,0），

当OP=PC时，点P（），

综上，点P的坐标是(10，0)或(-10，0)或（12,0）或（）时，是等腰三角形.